In this article we continue last month’s investigation of sandwich panel coupons using an Instron universal testing machine (UTM). There we laid out the basic setup for the tests and the types of information presented in the graphs, with a discussion of the first batch of coupons (2-core-2 with honeycomb core). Here we’ll continue our look into the remaining coupon tests, as well as explain the importance of derating thin-laminate coupons with a knockdown factor.
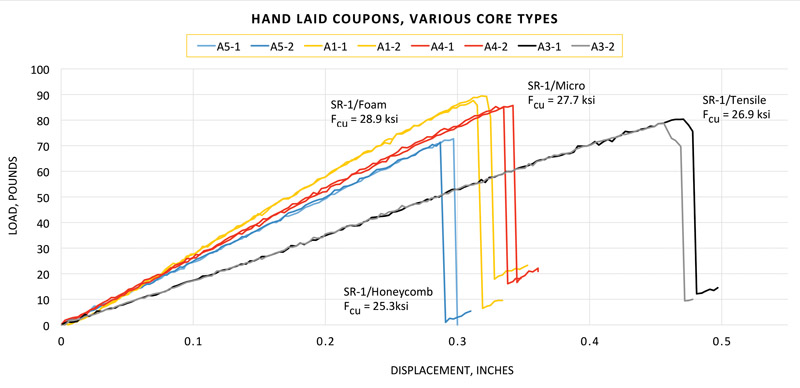
Graph 1 shows the results of various coupons manufactured by the SR-1 Project. The A5 coupons (blue lines—2-core-2 carbon/honeycomb) have already been discussed in last month’s article and are included here as a sort of baseline reference. The A1 coupons (yellow lines) are identical to A5 with the exception of being foam cored, rather than honeycomb. The A4 coupons (red lines) are identical to A5 with the exception of treating the top surface with wet micro. Finally, the A3 coupons (black lines) were an attempt to induce tensile failure by mounting a 2-core-1 coupon with the single ply on the bottom (in tension).
As expected, A1, A4 and A5 display similar stiffness and ultimate tensile strength. The foam-core coupon shows greater strength and stiffness compared to the honeycomb coupon. This was somewhat surprising (given the general perception of honeycomb as a “superior” core material), and is possibly due to the foam’s greater resistance to microbuckling (see more on this in the summary). The A4 micro-treated core falls between A1 and A5. I cannot think of any particular reason why micro would affect the strength of the coupon, and given the small sample number (2), I’d be hesitant to read anything into the slightly lower performance other than simple statistical scatter. That said, the micro does make the coupon heavier and thus slightly reduces the strength-to-weight ratio.
The attempt to induce tensile failure with the A3 coupons was unsuccessful, probably due to microbuckling of the upper facesheet in compression. The use of 3 plies on the upper surface would probably have been sufficient to force failure on the tension side, but since 2-core-1 is a layup schedule used in various parts of the SR-1, we were curious to see how that exact schedule would perform. The greater deflection is due to the greater flexibility associated with asymmetric facesheets. This is to be expected and can even be used by the designer to optimize part weight if the component sees asymmetric loads.
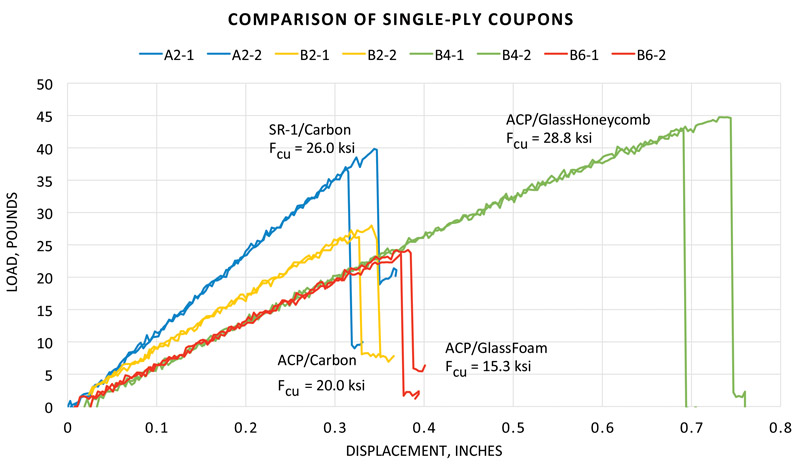
Graph 2 compares foam-cored coupons. As noted above, while the A1 coupons (blue) perform even better than their honeycomb-cored cousins (both stiffer and stronger), the performance of the manufactured coupons is puzzling. The B5 (black) coupons both failed from delamination, while the B1 carbon coupons are significantly less strong/stiff than would be expected. This, and the fact that the curves for both B5 and B1 are slightly non-linear, suggest problems with the core. Indeed, extreme flexure was observed to be the cause of delamination for the glass coupons. It was also observed that while all of the honeycomb-cored coupons display a sharp drop-off at Pmax (max load), the majority of foam-cored coupons manifest a “bull nose” near failure, possibly indicating the onset of core crushing. Any type of core problem invalidates coupon results under D7249 guidelines by which these tests were performed.
Graph 3 looks at single-ply coupons. The results generally mirror those seen in the two-ply coupons, with overall reductions in strength and stiffness associated with a thinner facesheet. The structural efficiency (strength to weight) of the single-ply coupons is less than double-ply coupons since they have half the load carrying facesheet but the same core weight.
Summary
First, let’s discuss the limitations of this kind of testing. I will repeat what I have stated in previous articles on coupon tests: The results you see here should be considered descriptive, not prescriptive. They should not be used for engineering design or analysis; they are for educational purposes only, to highlight differences you might possibly see when using various materials. The SR-1 panels/coupons are a product of a unique environment and preparation method, and may differ significantly from panels made by others elsewhere.
In addition, remember that the map is not the territory. Coupon failures or inadequacies do not necessarily reflect failures or inadequacies as they might relate to fabricating an airplane, only in fabricating a coupon. The opposite is also true: these tests are artificial, with loads very different from what panels in an airplane will see. In other words, Do your own testing!
The outcomes of these tests should also be viewed in light of the following serious limitations:
1. More than half of the failures occurred beneath the load bar, rather than between the bars. The ASTM chairperson for this standard admitted that failure beneath the bar is a gray area in terms of acceptability; if no core crushing is visible, and if the beneath-bar results pool with between-bar results, then the results may be acceptable. (Generally, these coupons showed no core crushing and beneath-bar results mirrored between-bar results).
2. The number of tests was not statistically significant. As such, the results should be considered merely anecdotal.
3. The standard specifies a test duration of between 3 and 6 minutes from the point of load application until coupon failure. Due to the very limited time in which we had access to the machine, our tests were accelerated and had a duration of between 35 and 65 seconds.
4. Beam theory assumes no excessive deflection. Excessive deflection is not defined by the standard, but the chairperson suggested that any deflection greater than 2 to 3 times coupon thickness be considered excessive. By this definition, several coupons, particularly the fiberglass-faced coupons, exhibited excessive deflection.
5. Loading bars should ideally allow free rotation of the specimen at the loading and support points (see picture of the lab-quality fixture on the opening page). Our fixture had fixed bars, and the slight lateral forces resulting from coupon deflection alleviate facing stresses, such that the observed ultimate loads may be artificially inflated. In addition, the use of round bars versus flat pads can result in local specimen crushing (which may have caused under-bar failure).
6. The Instron used was not specifically calibrated for these tests and exhibited a degree of non-linearity in the no-load position, resulting in a degree of error introduced into the measured results. The graphs shown in this article have been corrected to place curves at the origin, which has introduced a certain degree of error into the force/deflection curve.
All that said, the Instron testing was quite educational. First off, only 8 of 28 coupon tests would be considered valid under D7249 guidelines. That might seem like a pretty poor success rate, but it became clear that testing of thin laminates is somewhat tricky since they are relatively susceptible to local failure due to point loading from the fixture pads (I felt a little better when I read about one pair of researchers reporting success in only 12 out of 51 coupon tests). As pointed out above, the under-bar failures give results very close to the valid between-bar failures, and so may not need to be dismissed entirely.
We were surprised to see the SR-1 coupons outperform the manufactured coupons since the manufactured coupons are fabricated with prepreg laminates under tight quality control. The reasons for this are unclear.
Cal-Poly mechanical engineering senior and SR-1 Project intern Brian Paris manning the data collection station. The Instron can be seen in the background.
Microbuckling
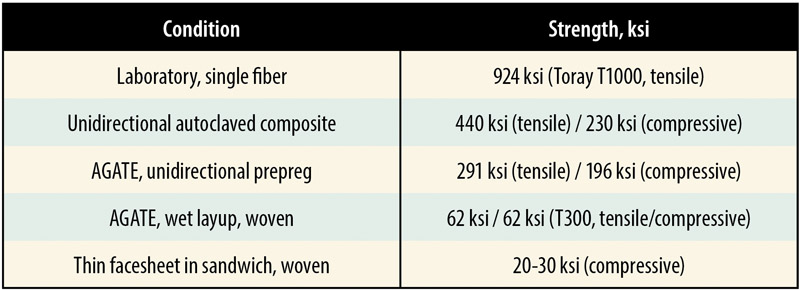
Those familiar with carbon fiber properties may find the low compressive strength surprising. Carbon can seem like a game of decreasing returns the more you know about it. On the surface, it’s amazing stuff—T1000 fibers show a tensile strength of almost 1000 ksi, i.e., 1 million psi (see table below). Then you realize these are individual fibers tested on razor blade balances in a laboratory. Workaday T300 (used in the Hexcel 282 plain-weave carbon fiber in these coupons) is closer to 500 ksi, but then you realize that that is the fabric alone. Once you add an epoxy matrix, the tensile strength drops to about 270 ksi (all that epoxy is “dead weight” as it were—it keeps the fibers straight and stiff, but doesn’t carry a significant structural load).
270 ksi is in thick (i.e., 10 or 12 plies) unidirectional laminates fabricated from prepregs processed in a high-temp, high-pressure autoclave. But doing a wet layup of woven cloth (where half the fibers are running perpendicular to the applied load, thus contributing nothing to compressive or tensile strength), vacuum bagged at 1 bar and room temperature? Now it’s down to 60 ksi. That’s no better than aluminum! And as you can see from these tests, the best numbers achieved (for carbon) for our coupons was 29 ksi. What gives?
What gives could be wrinkling (aka microbuckling). As the laminate becomes thinner and thinner, localized, small-scale buckling becomes the predominant failure mode. It’s not necessary to go into the details here, other than to say that the straighter and smoother you can make the skins of your sandwich structures, the better they will do. Predicting the critical stress when a facesheet will wrinkle has been the subject of much study, but one of the more common predictive equations is:
σ = k(EfEcGc)1/3
where:
k = “knockdown factor” between 0.5-0.91, with 0.5 being the most commonly used value.
Ef = elastic (compressive) modulus of the facesheet (i.e., elasticity of the facesheet).
Ec = core compressive modulus.
Gc = core shear modulus.
No need to break out in mathematical hives here—the point to be made is that you can increase your sandwich panel’s wrinkling threshold (σ) by either (1) increasing the facesheet modulus (i.e., choose a stiffer material for the facesheet like carbon over fiberglass), or (2) choosing a core that has higher compressive and shear modulus values (like simply using a denser core, say 6-pound foam instead of 3-pound foam).
Out of curiosity, we can compute the critical wrinkle limit for the coupons used in this test from the above equation. From the Divinycell data sheet for H100 foam core we find:
Ec = 19.6 ksi and Gc = 5.1 ksi
Determining the modulus for the facesheet is more difficult, since it depends greatly on how the laminate was made. We were unable to find modulus numbers for wet layup, room-temp bagged laminates, but Hexcel gives a number of 7400 ksi for their 282 woven cloth processed as an autoclaved prepreg. From experience, we know that we can expect an approximately 35% knockdown when using wet layup/1 atmosphere bagging as compared to autoclaved prepreg, thus giving
Ef ≈ 4810 ksi
So from the above equation, we find
σ = k(EfEcGc)1/3
= 0.5 x (4810×19.6×5.1)1/3
= 38.7 ksi
which is not terribly far off from the values observed in our tests, and definitely lower than the ~ 60 ksi compressive strength we see in thick laminates from the AGATE tests.
As mentioned above, foam cores may hold an advantage over honeycomb for thin facesheet sandwich panels since the empty space between honeycomb cells is theorized to possibly aggravate wrinkling (i.e., nothing is supporting the facesheet there), and we do indeed observe higher strength in the foam-cored coupons in this test. This is where the higher mechanical properties of a core like Rohacell can theoretically have a large impact. The data sheet for Rohacell 110 IG (roughly equivalent to Divinycell H100) gives
Ec = 23.2 ksi and Gc = 7.2 ksi
thus yielding
σ = 46.4 ksi
Even after accounting for 110 IG’s 10% greater density compared to H100, we would expect the final strength-to-weight ratio in our coupons to be about 15% higher with Rohacell cores. In fact, the SR-1 Project plans to investigate exactly that with this year’s summer interns.
Wrinkling could also explain why some of the fiberglass coupons in this test returned compressive strength values on par with carbon: Because the 8-ounce fiberglass facesheets were thicker than the 6-ounce carbon, they would hold out longer against wrinkling, thus allowing the fiberglass to realize a greater percentage of its potential compressive strength. That said, I would place that comment in the realm of pure conjecture since the failure mode of several of the fiberglass coupons was rather unpredictable, and I think more may be involved than just microbuckling.
For further reading on the above subject, I highly recommend Facesheet Wrinkling in Sandwich Structures (NASA/CR-1999-208994).
The Takeaway
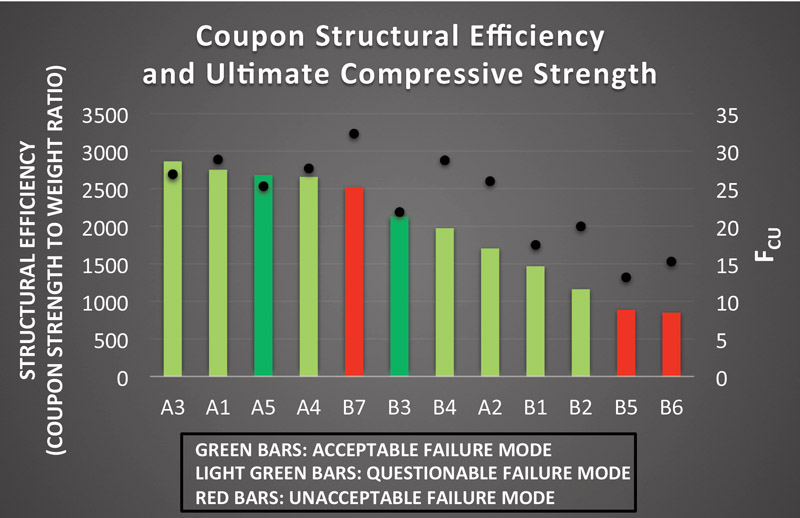
We’ll finish off this article with what most of you really probably want to know—which panels give the best structural efficiency, i.e., strength-to-weight ratio? For that, refer to Graph 4.
Graph 4. Structural efficiency (colored bars) and Fcu (black dot) for all coupons. Dark green bars indicate valid tests, light green indicates questionable validity, and orange indicates invalid tests (see coupon key in Part 2 of this series).
This last graph compares the strength to weight and observed ultimate compressive strength for the entire set of coupons. The strength-to-weight figure is derived by dividing the max coupon load by the coupon weight; it has no particular inherent meaning other than to allow a comparison of strength between approximately identically sized coupons (we say approximately since there are slight dimensional differences between coupons). The SR-1 Project panels all show compressive laminate strengths between 25-29 ksi, and the bog standard A1 panel (2-core-2 carbon/foam) tops the list for structural efficiency (the A3 was 2-core-1, so it has slightly higher efficiency but for tensile-oriented loads only). The performance of manufactured panels was more varied, though the reason is unclear.
An early reviewer of these articles suggested I end each article with a list of recommendations. Hopefully the limitations above will make clear why I have chosen not to do that here; there’s just too much variability in composites fabrication. Until one starts working in a very controlled environment (for example, an autoclave), with very controlled materials (like prepregs), and can regularly test coupons of your work, the best most builders can hope for is to include a healthy margin of safety in their designs. The downside to this is that some of the magic of composites is lost when the strength allowables and safety margins yield components that are no lighter than they would be in aluminum. That still leaves us with advantages like compound-curve, precision-molded parts, and with your own coupon testing, you may be able to trim a bit of fat off your design margins.
In the next article of this series, we’ll take yet another look at destructive testing, this time using scale models. Yes, we like breaking stuff!
Acknowledgments and disclosures: Many thanks to SR-1 Project sponsor Aerospace Composite Products for supplying the panels for the ACP coupons. Evonik, maker of Rohacell (mentioned in the article), is also a sponsor of the SR-1 Project. Also thanks to Brian Paris for his help with this month’s article. Brian is a graduating senior in mechanical engineering at Cal Poly, San Luis Obispo. He holds a Private Pilot license and was the 2015 Summer Intern for the SR-1 Project.
![]()
Eric Stewart is designing and building the SR-1, a speed plane for setting records in the FAI c-1a/0 category (takeoff weight less than 661 pounds, including pilot and fuel). You can see more at facebook.com/TheSR1Project, including additional photos and videos of the subjects in this series of articles.