Last month we looked at how the aerodynamic forces acting on an airplane can be described with nondimensional quantities that are independent of airspeed and air density. In addition to describing the forces on the airplane in a nondimensional fashion, we need to similarly characterize the conditions in the free-stream airflow. Dynamic pressure alone does not give enough information to ensure that we can match the flow conditions of a given test.

To get data at various Mach and Reynolds numbers, you can buy yourself a wind tunnel. Or maybe its better to just think about it.
Mach Number
There are two phenomena that affect the way air flows over an object, and they must be taken into account in all aerodynamic measurements. The first is called compressibility. When air is flowing relatively slowly (well below the speed of sound) it behaves like it is incompressible. This means that the density of the air remains constant everywhere in the airstream regardless of the change in pressure. This is only strictly true at zero airspeed, but compressibility effects are so small that they can be neglected at low speeds.
At higher speeds, the character of the airflow begins to change, and the air no longer behaves incompressibly. This causes the aerodynamic forces on the airplane to also change, even if the angle of attack and dynamic pressure are held constant. When the local airspeed at any point in the flow exceeds the speed of sound, shock waves form, causing even more dramatic changes in aerodynamic forces.
Measuring airspeed alone is not sufficient to properly take this into account. We also need to know the relationship between the free-stream airspeed and the speed of sound. The nondimensional parameter that tells us this is the Mach number (M), which is the airspeed divided by the speed of sound in the free-stream atmosphere surrounding the airplane. The speed of sound varies with altitude and temperature, so it is important to make sure that M is computed using the correct local atmospheric conditions.
Aerodynamic data taken at one M is not necessarily applicable to flight at a different M. The variation of aerodynamic behavior with M is small at low speeds, but as M increases, compressibility effects become more important. In general, at Mach numbers greater than about 0.6, compressibility must be taken into account, though there are some configurations where compressibility effects appear at even lower Mach numbers.
Reynolds Number
The second phenomenon of concern is viscosity. Although air is thin compared to maple syrup, it is still a viscous fluid. It is the viscosity of the air that gives rise to the boundary layer, and causes skin-friction drag and flow separation. What the aerodynamicist needs to know is how strongly this viscosity is affecting the airflow.
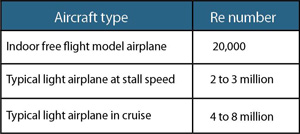
Typical Reynolds number values.
As air flows over a surface, two sets of forces are in action, opposing each other. The momentum of the air tries to keep it moving, and viscous friction tries to stop it. The relative strength of the two phenomena determines the nature of the boundary layer and also affects the outer flow through the thickness of the boundary layer and flow separation.
The Reynolds number (Re) is a nondimensional quantity used to characterize this phenomenon. It is directly proportional to the size and airspeed of an object moving through the air, and is inversely proportional to the kinematic viscosity of the air. The Reynolds number is based on a characteristic length associated with the object. For airfoils and wings, Re is based on chord. For bodies of revolution, diameter is commonly used. Kinematic viscosity is a physical property of air that relates density and viscosity. Values of kinematic viscosity can be found in a standard atmosphere table.
The same object can have radically different aerodynamic characteristics at different Reynolds numbers. A classic example is a smooth sphere, which has a drag coefficient of about 0.47 at Reynolds numbers from 1000 to 4×105 but about 0.10 at higher Re. At this critical Re, the position of flow separation on the sphere moves aft, making the wake smaller and decreasing drag. Airfoils can exhibit similarly dramatic changes in stall characteristics as Re changes.
The lower the Re, the more viscous the air appears to the airplane. For a given type of boundary layer (laminar or turbulent), skin friction will decrease as Re increases. Increasing Re makes it harder to maintain laminar flow, but easier to maintain attached flow. (Re values are shown in the table.)
For two airflows to be truly similar, both Re and M must be the same. This is one of the major difficulties engineers must deal with when using wind-tunnel data. Wind-tunnel models are much smaller than real airplanes, so the airspeed must be higher to match Re. Unfortunately, this causes a mismatch in M. Years of history have taught us that, particularly for high-speed airplanes, it is much easier to correct data for differences in Re than for differences in M. Accordingly, when doing high-speed testing in an atmospheric-pressure wind tunnel, we always run at the proper M, and correct the data later for Re effects. Reynolds number effects are why data from small wind tunnels tends to be misleading. This is not good news for those of us who would like to have our own pet wind tunnel to play with at home.
There are ways to get wind-tunnel data at the correct M and Re, but they are all expensive. One way is to build a huge wind tunnel and test full-scale models. NASA has such a facility at the Ames Research Center. It has two test sections. The first has a cross section of 40×80 feet, and the second has a cross section of 80×120 feet. This tunnel can reach airspeeds on the order of 300 knots, and pulls as much power as a small city when it is running.
Another approach is to change the properties of the air rather than the size of the model. This can be done by either pressurizing the tunnel, or by chilling the air in it to cryogenically cold temperatures with liquid nitrogen. There are tunnels that use both of these concepts in operation. All produce high-quality data, but at a high price. The majority of testing is still done in atmospheric-pressure tunnels, and aerodynamicists spend many hours working to apply the data properly to predict the characteristics of the real airplane, which flies at a higher Re than was achievable in the tunnel.

![]()
Barnaby Wainfan is a principal aerodynamics engineer for Northrop Grummans Advanced Design organization. A private pilot with single engine and glider ratings, Barnaby has been involved in the design of unconventional airplanes including canards, joined wings, flying wings and some too strange to fall into any known category.













