We found out two months ago in May that there is a chip that will take a voltage and make a graph-like display, then last month we figured out ways of making that display out of some readily available 3-millimeter light-emitting diodes (LEDs) and some really tiny 0805 LED surface mount devices.
It has now come time to figure out how to convert physical quantities like oil temperature and fuel quantity into the voltage to feed that chip we talked about in May. In general, we use sensors that change resistance with a change in physical quantities. For example, to sense oil temperature, we use a little chunk of carbonized material called a thermistor. A thermistor changes the resistance of the carbon as a direct function of how hot it gets. We use this resistance change to move a needle on a gauge calibrated in degrees Fahrenheit or Celsius. For fuel quantity, we bolt a float onto the rotary shaft of a “volume control” that, again, moves a needle on the instrument panel calibrated in gallons, liters, pounds, or kilograms—your choice.
Our job this month is to convert those resistance changes to a voltage to drive the LM3914 chip. That may seem like a pretty trivial task until you talk to a real expert in the field of aircraft sensors. I asked instrument guru Bob Lasecki of Mitchell Products about fuel senders and got this bit of information:
“There are a number of ‘standard’ fuel sender resistance ranges in existence. Mooneys and Bonanzas are typically 0 ohms empty and 30 ohms full. Many Pipers are 240 ohms empty and 33 ohms full. Another common range is 10 ohms empty and 180 ohms full. Tip tank senders are commonly 0 ohms empty and 90 ohms full. Besides these ‘standards,’ there is a plethora of variants with electronic sensors having a converter module that produces 0 to 5 volts for empty to full, and some systems that have boards with resistance networks to balance multiple senders per tank to give a composite reading. Cessna has been known to change fuel system wiring (and resistance) as many as four times per model year, so the only way to know what you have is by inspection and measurement or by serial number if you can find someone to trace it for you.”
And I thought this was going to be an easy task. Sigh. At least one of the things I knew I wanted to do is a standard…0 volts empty (or minimum temperature) to 5 volts full (or maximum temperature). Zero volts for no flaps to 5 volts for full flaps, and so on.
What that means in our world is that I’m going to have to give you a generic “make it like this” for any possible combination of resistance values and methods of how that resistance changes. Let’s start off with some reasonable approximations.
First, I want no more than 1 volt across that resistance under any circumstances. I also want that 1 volt to be the maximum input to the instrumentation amplifier I’m going to tell you how to make. Let’s figure out how to do that. Again we borrow from Brother Ohm, who told us that voltage is the product of current times resistance. Doing a bit of algebra on that equation, we find that current is voltage divided by resistance. What does that mean? For example, take our Piper example that has 240 ohms empty and 33 ohms full. If I want no more than 1 volt across this sensor, then the current should be 1/240 of an ampere, or 4.2 milliamperes. At full, then, the voltage across the sender will be 4.2 milliamperes (4.2 mA) times 33 ohms, or about 0.14 volts.
Now we can start to solve the problem. First, how do we get 4.2 mA of current? We could do it by brute force and stupidity simply by running the sender from the 12-volt aircraft supply through a 2.6kΩ resistor, but that presents a couple of problems. First of all, the closest standard value I can buy is 2.7kΩ. Second, and even more difficult, is that this sender needs to indicate correctly no matter whether the battery supply is 12 volts (engine off) or 14 volts (engine on and alternator running). That will let the current vary from 4.2 mA to 4.9 mA, a 16% variation. Or, to put it another way, on a 50-gallon tank that is an error of 8 gallons. Not acceptable.
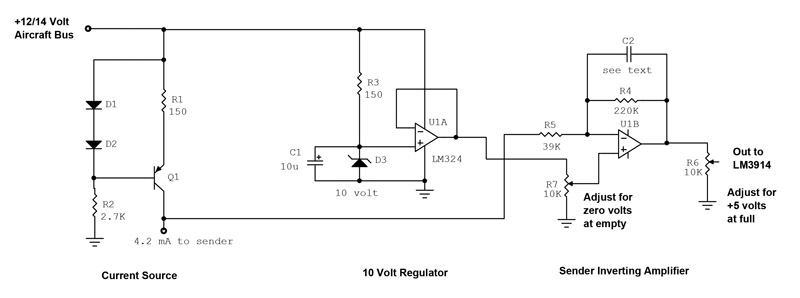
So we revert to an old trick called “throw a transistor at it.” The circuit shown provides 4.2 mA to the sender under nearly any condition of power supply voltage, temperature, and circuit variations. It is called a PNP current source and is one of the most useful configurations that we have in electronics. I’m not going to go into the theory of things, only to point out that the two diodes in series (D1 and D2) can be replaced with a single LED that will serve as a pilot light. R1 will also have to change in value, and if we go into that calculation, we will be into the August column before I’m done (hint—it is a function of the color of the LED). However, in the circuit shown, Q1 can be any “floor-sweepings-quality” PNP transistor, and the same for the two diodes so long as they are plain-jane silicon devices. R1 can be any wattage you have lying around.
So, we have Mr. Piper’s sender giving us a voltage output of 1.01 volts empty (240Ω * 4.2 mA) and 0.08 volts full. That’s a “span” of .93 volts. But we want 0 to 5 volts to drive the IC. And, it has to be reversed so that full is 5 volts and empty is 0 volts. We need, then, an inverted gain of 5.4 to achieve this. How, you ask? With our old friend the op-amp, shown in the circuit.
U1A is a simple 10-volt regulator to keep the “calibrate” voltage for R7 constant. Note that if I was to actually go into production on this design, I’d use another current source PNP transistor circuit in place of R3 just to provide the best precision I could to the readout.
U1B is an inverting amplifier with a gain determined by the ratio of R4 to R5. We said that we wanted a gain of 5.4, and R4/R5 gives a gain of 5.6. This is a little more than we need, but with R6 setting the output to less than maximum, that should be just about right.
C2 deserves a bit of discussion. It is an “anti-slosh” capacitor. Rather than having our readout jumping all over the place as the gas sloshes around in the tank, C2 serves to keep the output voltage relatively constant over a reasonable time period. What is reasonable? The product of R4 (in megohms) and C2 (in microfarads) sets a “time constant” that keeps the output from jumping around. For example, if you chose C2 to be 100 microfarads, the time constant of these two parts would be 22 seconds. That’s a reasonable slosh factor, but is adjustable to nearly anything you want. There are a dozen ways I can think of to make this time constant anything you wish; that could be a column completely unto itself.
Ah, spring is nearly upon us, and a young man’s fancy turns to wine, women, and song. But for us old geezers, it is Cessna, Van’s, and Rutan. How about using one of those old Harbor Freight solar cells to keep the battery up to snuff between flights? Or maybe we can talk about ADS-B in simple terms. It is going to be a great summer. Have fun, see you at The Show…and…Stay tuned…

![]()
Jim Weir is the chief avioniker at RST Engineering. He answers avionics questions in the Internet newsgroup www.pilotsofamerica.com-Maintenance. His technical advisor, Cyndi Weir, got her Masters degree in English and Journalism and keeps Jim on the straight and narrow. Check out their web site at www.rst-engr.com/kitplanes for previous articles and supplements.