In the last part, I discussed the way loads on a structure can be calculated if you know the external load. Our basic example was a cantilever beam that we assumed was fixed at the left end and free at the right end.
But some structures aren’t conveniently fixed or cantilevered at the left end. Some, like biplanes and strut-braced wings, not only aren’t fixed at the root, they have a load from the strut. This situation is more complicated. We know that if a structure is hinged, that it can’t carry any moment at the hinge. That’s fundamental. But what about the strut—what effect does that have on the load distribution across the spar?
For a spar that’s hinged at the root and has a strut, we need to find the moment at the root as if it were a cantilever beam with no strut, as we discussed in Part 1. Then, since it does have a hinge, you would calculate the load perpendicular to the spar where the strut connection is, by dividing the cantilever bending moment by the distance between the root pin (the hinge) and the strut fitting.
The next step is to determine the moment and shear load anywhere along the spar.
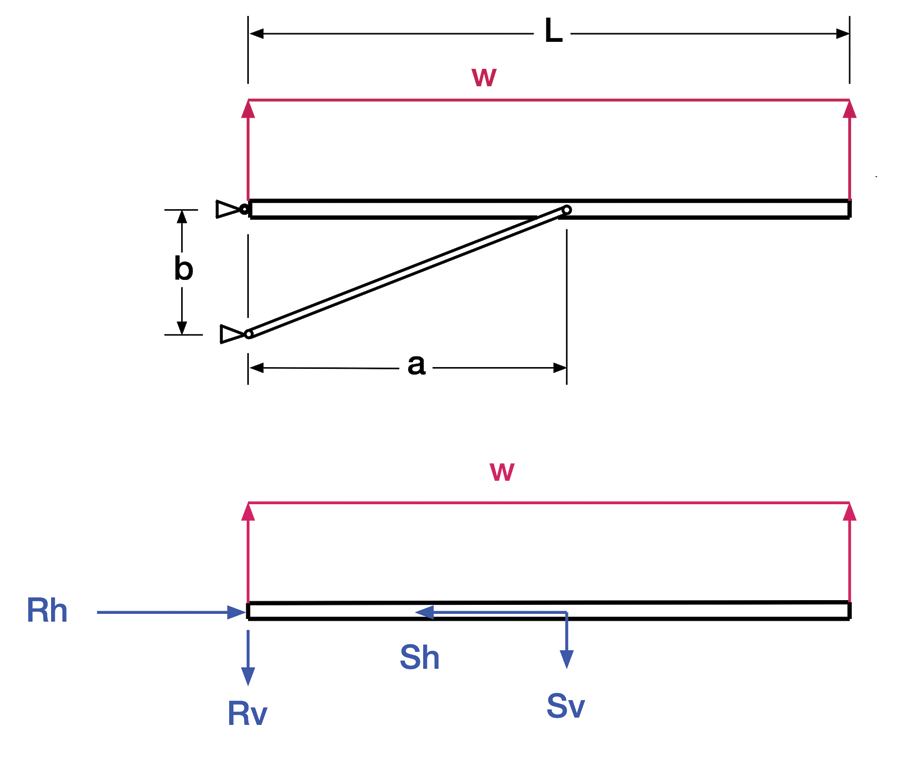
The top sketch of Figure 1 shows a uniform running load “w” on the spar of a strut-braced wing. The fuselage attachment fitting is on the left, and the strut attaches to the circle in the middle of the spar. The load in the example is a uniform load. We learned in Part 1 how to calculate the loads on the spar for this kind of applied load, applicable to the outboard portion of the spar, and assuming a constant load has the additional advantage of simplicity. For a real spar we’d use the real load.
The upper sketch in Figure 1 shows the physical structure and its load. The lower sketch is a free body diagram that shows the spar with the applied load “w” and the reaction forces from the strut and the hinge at the root. I’m writing the reaction forces with “R” and the strut forces with “S,” and using “h” for the horizontal components and “v” for the vertical components.
The first thing to do is find the forces on the strut. The moment at the left end of the spar, if there weren’t any strut and it were fixed there, would be:
M = 1/2 * w * L2
Where
M = Virtual cantilever moment at the left end, inch pounds force
w = constant running load, pounds force / inch
L = Total length of the load, inches
The load Sv is the vertical component of the load on the strut.
Sv = M / a
Where
Sv = Vertical component of the strut load, pounds force
a = Distance, left end to the strut fitting, inches
In a pin-ended rod like a strut, the force always goes through the pinned ends, since neither end can carry any moment. This means that the components of that load are proportional to the components of its length. In this case, that means that
Sh = Sv * a / b
Where
Sh = Horizontal component of the strut force, pounds force
b = Distance, vertically, left spar hinge to strut bottom fitting, inches
We can find the load in the strut by Pythagoras’ Theorem:
Strut Force = (Sh2 + Sv2)1/2
The strut force is also in pounds force.
If the bottom of the strut is located some distance forward or aft of the spar, you’ll have to find that component of force the same way and include it in the strut force equation.
The next step is to determine the vertical reaction force at the left end. Since the forces must balance, we find the total shear force. Knowing Sv,
Rv = w * L – Sv
Where
Rv = Vertical component of the left load on spar hinge, pounds force.
If Rv is negative, the vertical reaction load at that point is up instead of down—which could happen; it’s affected by the actual load distribution and the location of the strut on the spar.
Next, for the inboard section between the root fitting and the strut, we need to find the moment and shear loads adjacent to the strut fitting on its outboard side. This represents the most inboard or left-most point of the cantilevered part of the spar. Here, the moment is
Mr = 1/2 * w * (L – a)2
and the shear force there is
Vr = w * (L – a)
Where
Mr = Moment immediately outboard of the strut, inch pounds force
Vr = Shear immediately outboard of the strut, pounds force
Inboard, between the two fittings, we need to look up the Aerospace Structures Manual, section B4.0.0, especially table 4.1.1-2, particularly load cases 13 and 15. Kitplanes has it here: asm-B400.
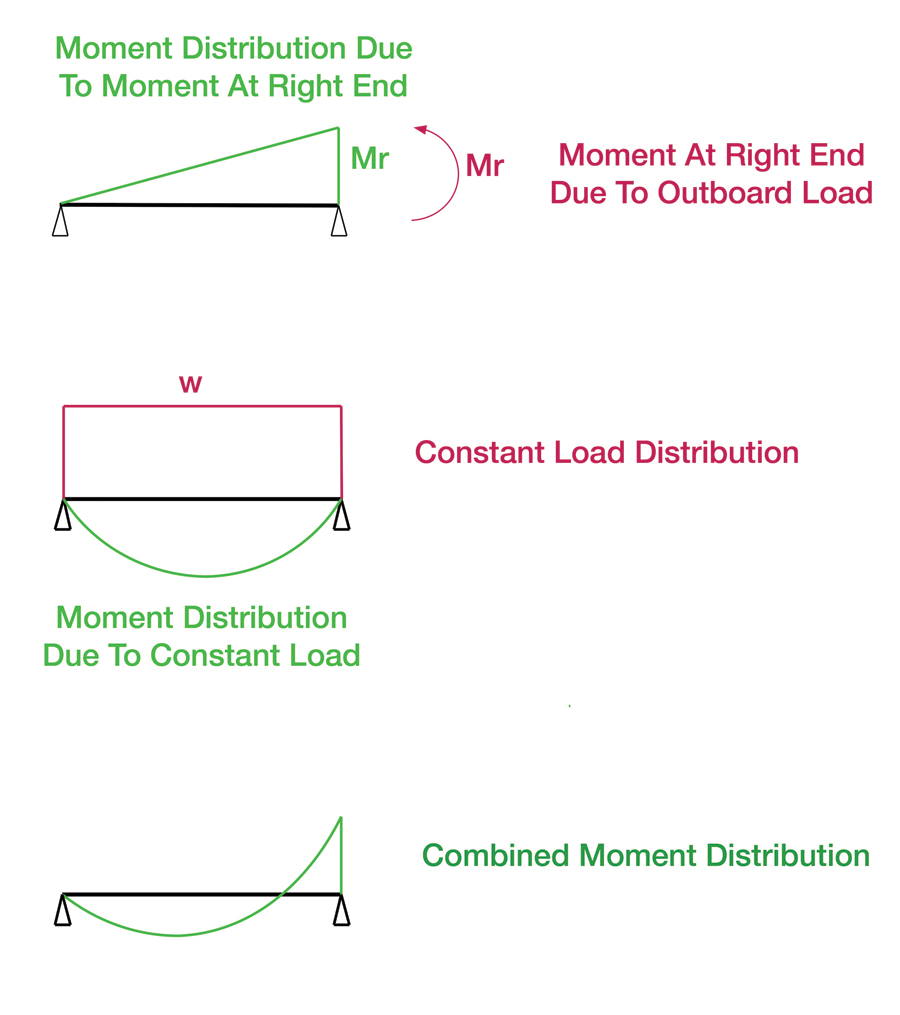
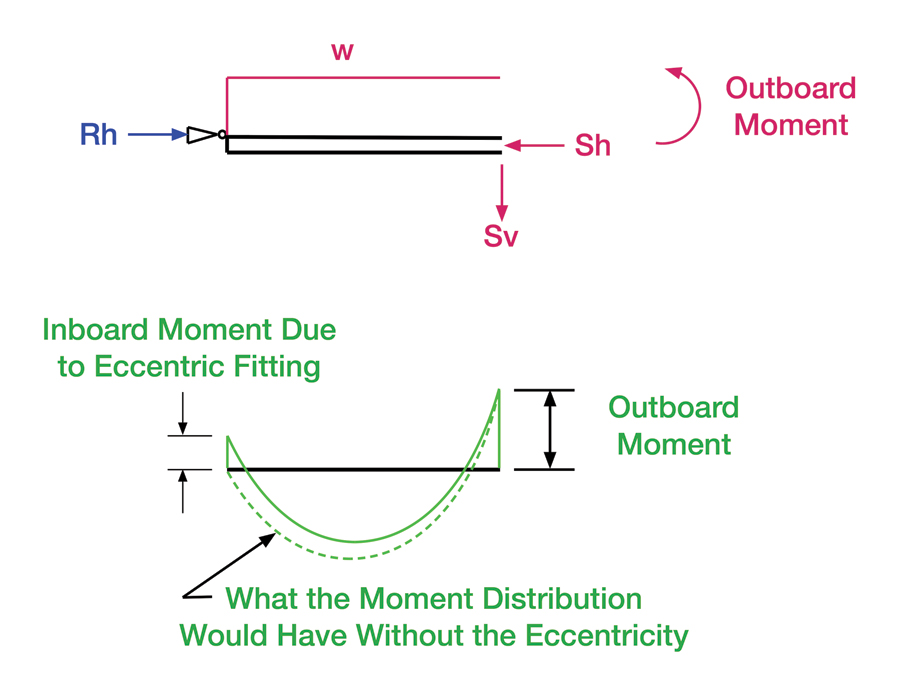
The top sketch in Figure 2 shows how the moment “Mr” from the outboard portion of the spar is distributed between the strut and the left end. At the left end, there is zero moment because that end is a pinned end. The moment load has a linear distribution between the strut fitting and the root hinge.
Figure 2: The inboard portion of the spar, between the root and the strut, is influenced by the moment from the outboard section and the moment generated by the inboard portion of the applied load. These are shown separately here.
The middle sketch shows the moment distribution from the constant load, from Aerospace Structures Manual. Note that its sign is opposite that of the moment from the outboard side, since it’s below the line. Be sure to keep track of that.
These moment distributions are superimposed, as shown in the bottom sketch.
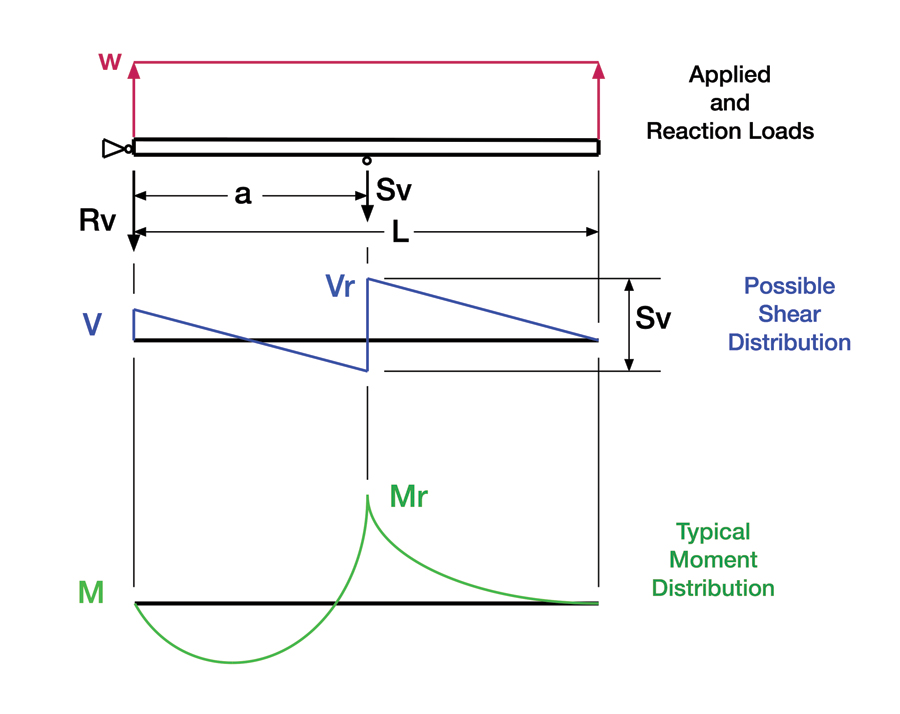
The shear distribution is interesting. In Figure 3, it’s the middle sketch. “Vr” is the positive peak (that is, above the line) of the shear load, just outboard of the strut. Then the strut load gets added in. The blue vertical line at “Vr” is the vertical component of the strut load “Sv.” The shear distribution inboard of that is due to the distributed load “w.” In the load and shear diagrams, I drew the inboard shear load as if it were positive, and so its reaction force “Rv” is shown negative.
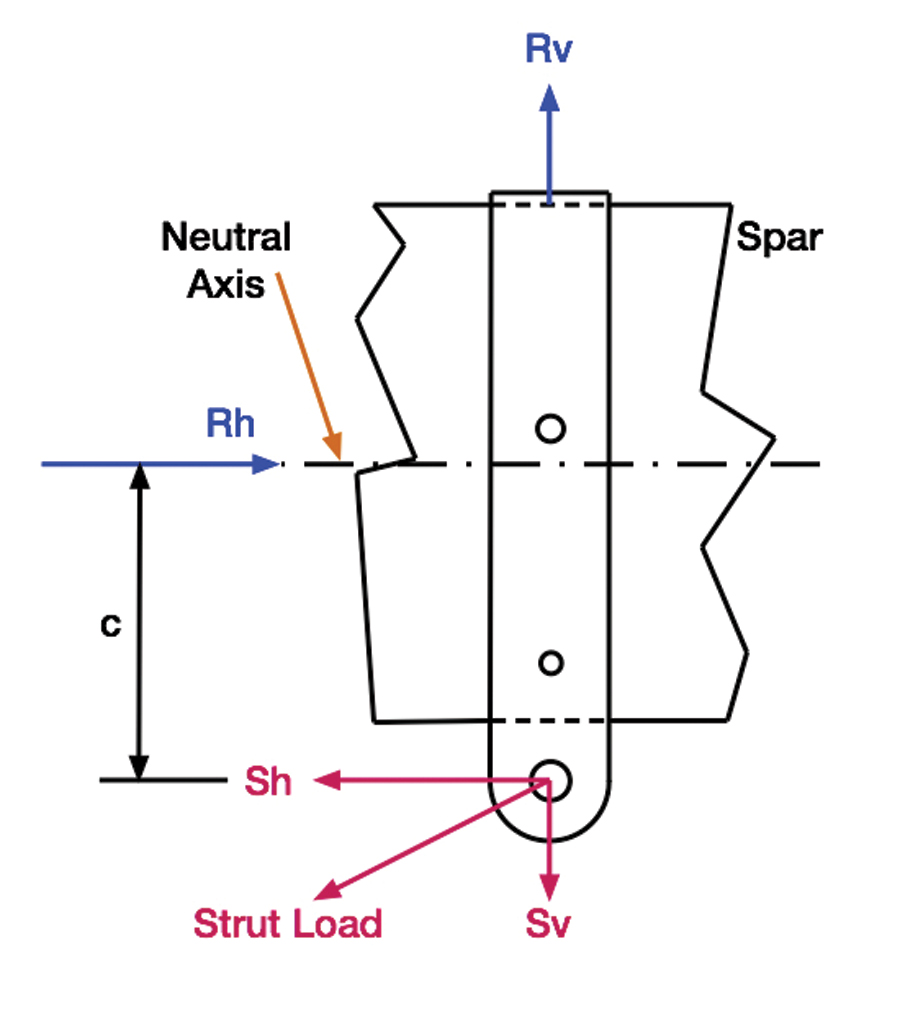
So far, we’ve been looking at a spar that has its strut fittings and its inboard (left end) fitting centered vertically on the neutral axis of the spar. Now let’s look at a strut fitting which puts a local moment into the spar.
As long as the strut fitting lines up with the strut, the fitting will act as if it is attached at the neutral axis on the spar, even if its attachment point is located below the wing. In that case, the strut load isn’t offset from the fitting, so the fitting doesn’t have any moment arm to generate a bending moment at the spar—the line of action of the force in the strut is directly through the centroid of the fasteners of the fitting to the spar. The term commonly used to describe this condition is zero eccentricity. In this context, the word “eccentricity” means that there’s some offset in the joint that, combined with the force in the joint, creates a moment. Generally speaking, these extra moments due to eccentric joints need to be considered. They sometimes show up in poorly designed joints where they add to the stresses in the joint and contribute little that’s good. Zero eccentricity means that there’s zero offset and therefore zero addition moment.
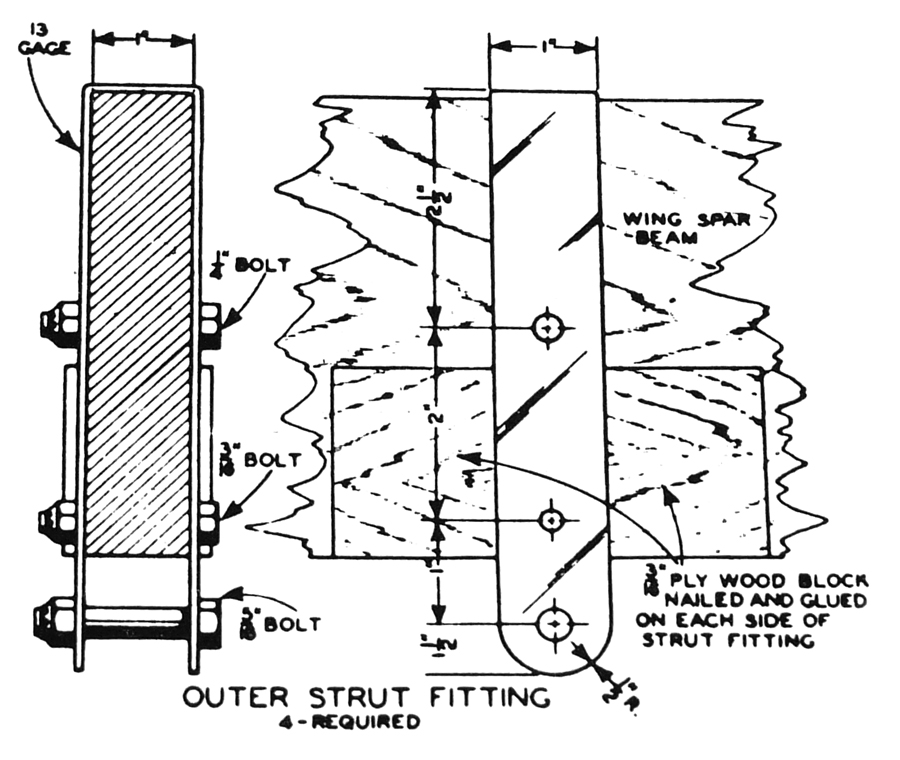
Figure 4: The Pietenpol strut fitting as shown in EAA’s 1932 Flying and Glider Manual. While simple, it imposes a local eccentric moment on the spar.
The classic Pietenpol Air Camper was originally designed with a highly eccentric strut fitting, shown in Figure 4. Imagine that the strut is attached to it and that the strut is angled so that it goes to the lower left. The fitting’s force loads are nicely carried by the plywood plates and the fact that the fitting goes over the top of the spar. The force balance is quite neatly done. The geometry governing the eccentric moment, shown in Figure 5, is
Me = c * Sh
Where
Me = Local moment on the fitting, inch pounds force
c = Arm for the eccentricity, inches
Sh = Horizontal component of the strut force, pounds force and must be carried by the spar.
Figure 5: The force reactions on the Pietenpol strut fitting, although we don’t know how the reaction force Rh will be shared between the bolt and the plywood plates.
In this case, for a positive flight load, it puts the lower edge of the spar in compression. That’s the opposite of moment load that the flight load on the outboard portion of the spar puts in. Note that the moment in the spar is based on the parallel component of the strut load “Sh” and the distance to the neutral axis of the spar.
I drew Figure 5 showing one way to define the eccentricity. The more formal way would be to measure it perpendicular to the strut axis and use the full strut force for the load. Pay attention to the sign of the resulting moment, of course, and that will work as well as this method.
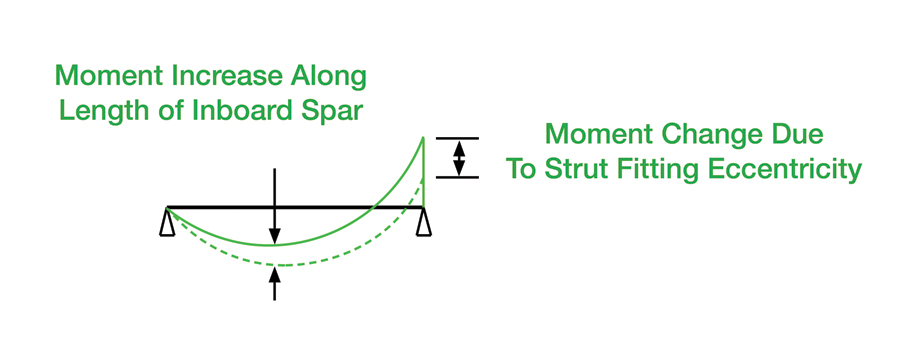
The effect of this eccentricity is shown in Figure 6, where the peak moment immediately inboard of the fitting is reduced by the eccentricity, and the moment along the inboard span is increased. These things, and the difficult moment-carrying design of the strut fitting, are issues that you’ll have to assess. The moment “Me,” along with what’s usually a considerable strut load, must be carried by the fasteners that attach the strut fitting to the spar.
Figure 6: The effects on the bending moment inboard of a strut fitting that’s not oriented along the strut axis.
What about off-center inboard end attachments, such as the Super Cub wingroot shown above? An eccentric joint can be designed into a structure and used for a specific favorable purpose. In the case of this wing, the fittings are located above the neutral axis of the spar. Remember from Figure 1 that an upward aerodynamic load on the wing develops an inward axial force due to the angle of the strut. That, combined with this eccentricity, results in a moment at the wingroot that puts the upper side of the spar in compression, just like the moment outboard of the strut—a positive bending moment. This moment is the opposite sign of the moment that is typically located in the mid-span of the inboard portion of the spar, and thus reduces magnitude of the negative moment, developed by the air loads, inboard of the strut.
If the perpendicular distance between the neutral axis of the spar and the inboard fitting is “d,” then the root moment becomes:
Mroot = d * Rh
Where
Mroot is the moment generated by the eccentric fitting in pounds force.
d is the eccentricity, inches, from the spar’s neutral axis, positive above the spar’s neutral axis.
Rh Reaction force parallel to the spar, pounds.
This design detail works best for longer inboard sections. For very short ones, with the strut fitting close to the fuselage, the moment from the outboard part of the wing dominates since the inboard section doesn’t have enough length to build up a significant negative moment. This illustrates that each aspect of the design of a strut-braced spar needs to be considered as part of the whole wing.