It’s probably not hard to believe that a straightforward way to determine your aircraft’s climb performance is to go out and perform climbs. The “sawtooth” climb flight test technique works very well but takes a lot of time. If you own your own airplane, maybe that’s OK; after all, you log it by the hour. However, a less intuitive but more efficient way to determine climb performance is to use the “level acceleration” method.
Sawtooth Climbs
Before getting into the level acceleration flight test technique, a brief overview of the sawtooth climb method is in order. The basic approach is to perform a climb over a measured change in altitude at constant airspeed. You measure the time to climb the known height and convert this to a climb rate. On a nonstandard day, you can measure the outside air temperature (OAT) and make appropriate corrections. You repeat this process varying airspeed and then plot the resulting rates of climb versus airspeed to determine the best angle and rate of climb. An advantage of this technique is that the flying and data reduction are easy. The downside is that you need about 10 good climbs to define the full curve, and this takes me over an hour to achieve at a single weight and altitude. If you want to define a climb profile (determine how VX and VY vary with altitude), you are going to invest several hours in climbing and descending. Or…if you’re tight on time or want to conserve fuel, you can try a different approach.
Rate of Change of Energy
You add energy to your plane by burning fuel. Imagine that the energy from fuel burnt can increase potential energy (height) or kinetic energy (velocity) at the same rate. This equivalence will allow us to measure the rate of change of velocity in level flight (acceleration) and then at any airspeed calculate an equivalent rate of change of height (rate of climb). In about an hour I can test the climb rate of my aircraft over its entire altitude range. The downside to this quicker test method is that there is some math to do after the flight. The good news is you only need to get the equations right once and then you can let a software tool like Microsoft Excel do the hard work for you.
Flight Profile
For this flight I took off with 30 gallons of fuel, which put the start weight at 1500 pounds (mid) and cg at 80.0 inches (forward). I flew a level acceleration at 2, 6, 10, 14, and 18,000 feet pressure altitude, which covers the practical operating altitudes of the RV-8.
Flight Test Technique
The setup for a level acceleration starts below the test altitude. You need to start far enough below the test altitude for the engine and airspeed to be stabilized—500 feet will do the trick with RV-like performance.
The airplane is slowed to just above the stall and then a climb is commenced with maximum continuous power. I used wide open throttle, 2500 rpm, and mixture leaned to 1200 F EGT. To properly identify VX and VY, it is necessary for the acceleration to start at an airspeed slower than both these speeds. This means you will need to be close to the stall during the setup climb to the test altitude. As you reach the test altitude, lower the pitch attitude quickly to transition to level flight and accelerate.
Rather than a nice gentle level-off that starts at 10% of the rate of climb before the test altitude, wait until 2.5% of the rate of climb. For example, if the climb rate is 1000 fpm, don’t start leveling off 100 feet before the test altitude; wait until you are about 25 feet below. Try to maintain the test altitude as closely as possible. A good scan of the aircraft pitch attitude, EFIS velocity vector or flight path marker, VSI, and altimeter is required. If your height wanders up or down a little, it is better to stay at the new altitude rather than correcting back to the target. Concentrate on holding altitude as you accelerate from just above the stall out to the maximum level flight speed at that altitude.
Due to the large airspeed change, you will need to trim, and there are two ways you can do this. First, you can trim during the climb and then continuously run the trim forward/nose down as you accelerate. The advantage to this method of trimming is that the trim tab (and hence trim drag) is always in the correct position for the speed you are at; hence the purists would argue it is more accurate. The disadvantage is that it is hard to trim precisely as the speed is rapidly changing, which makes it harder to maintain a constant altitude. Second, you can set the trim for the maximum speed, slow down and do the climb holding back pressure on the stick and then relax the back pressure as you accelerate. I personally find the second method easier.
Data Reduction
Post flight you are going to have to identify the part of the data recording that includes the various accelerations. The best way to do this is to note the time just before you start the climb and then again after the acceleration is over. On my Dynon SkyView the time recorded in the user data log is the Zulu time, so I use that as my reference. An hour of flight time recorded at 1 Hz results in a 3600-line spreadsheet, which is unwieldy to work with. Rule 1 is never touch the raw data. Always make a copy first and then manipulate the copy.
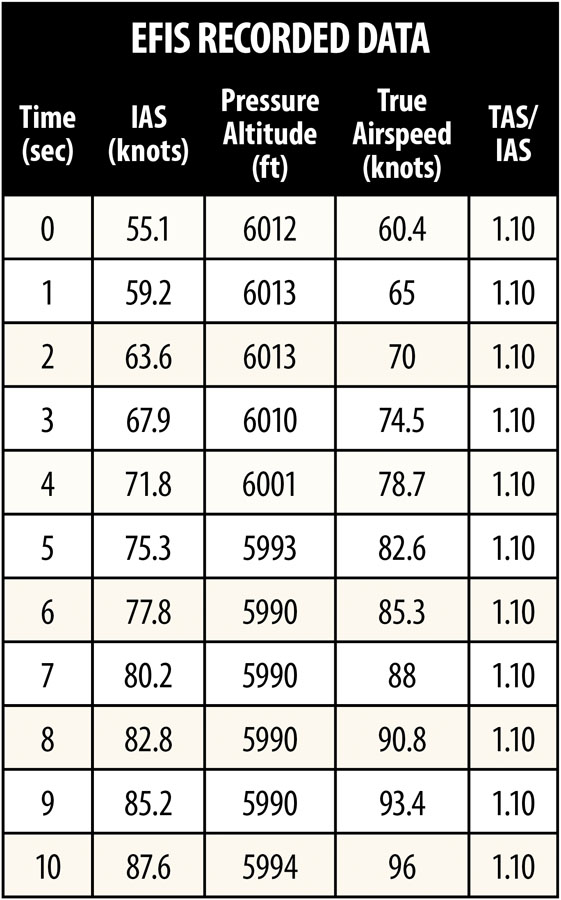
Once you have a copy, delete everything before and after the data point of interest. This will reduce the 3600 lines down to around 180 lines. Next you can delete all the columns/parameters that are not related to this test. Again, this makes it far easier to work with. The columns you will need are pressure altitude, indicated airspeed (IAS), and true airspeed (TAS). Add a new column for elapsed time, starting at zero and incrementing at the time between each sample of your EFIS (e.g., if you are recording at 1 Hz, increment the time by 1 second). Next, plot the altitude and true airspeed against elapsed time. This should look like the “Altitude & Airspeed During Level Acceleration” graph.
You are only interested in the data starting from when you level off until you reach maximum speed, so you can further trim away the data from the climb before you level off and after maximum speed is reached. In the example, I deleted data before T=23 seconds and after T=140 seconds. This reduced data set will look like the example of EFIS recorded data (note that only the first 10 lines are shown). The last column is the ratio of TAS/IAS; you will need this later to convert TAS back to IAS.
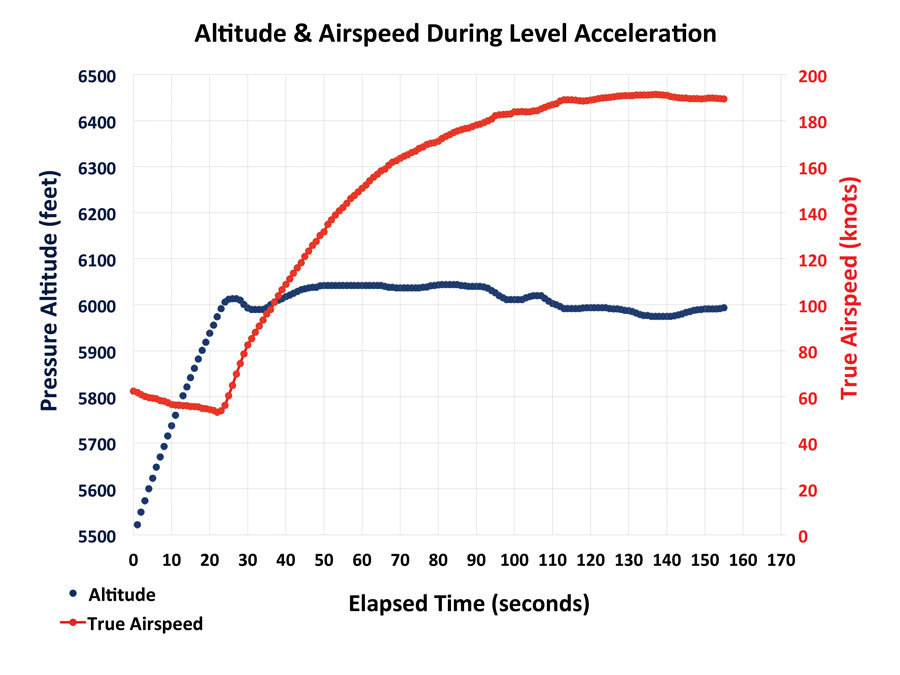
Now, plot this reduced data set of true airspeed against time (with time = 0 as the first data point). This will look like the “True Airspeed v Elapsed Time” graph. The TAS data probably won’t be a perfectly smooth curve due to little ups and downs in altitude while you accelerated. In my case I initially let the altitude climb by 40 feet and then dropped 20 feet low toward the end. Ideally, you would like to keep these altitude excursions to less than 25 feet. You will iron out these fluctuations by adding a trend line to the TAS data. Use a polynomial of 4th order, and display the equation with at least five significant figures. Now you will use the trend line polynomial equation to generate a smooth relationship of TAS versus time, starting from the lowest speed as you leveled off to the maximum speed.
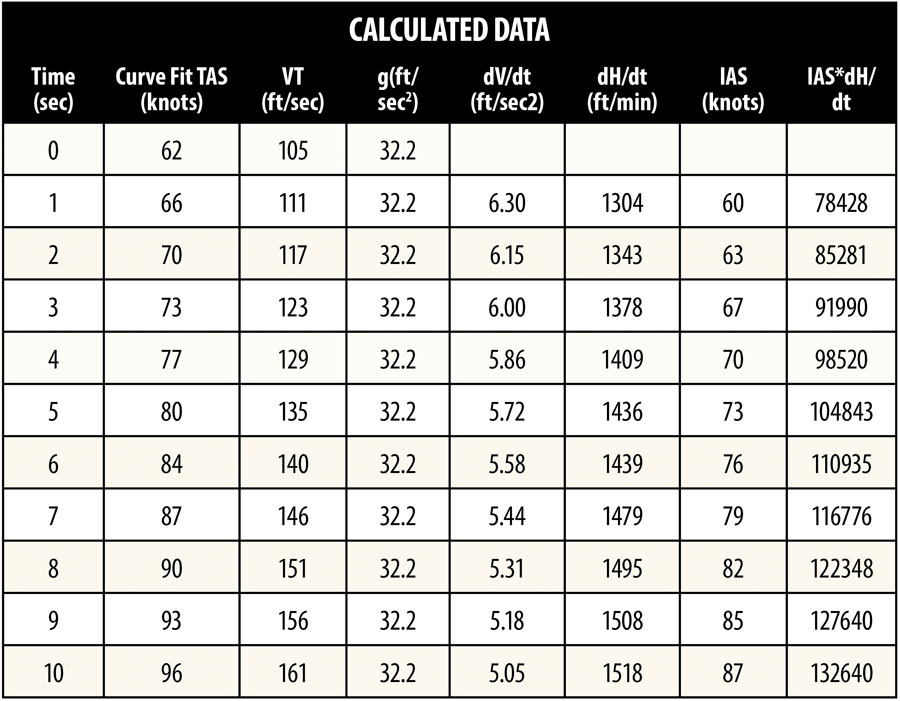
The next step is to use the trend line true airspeed versus elapsed time equation and convert to rate of climb. An example of the steps used is shown in the “Calculated Data” example spreadsheet.
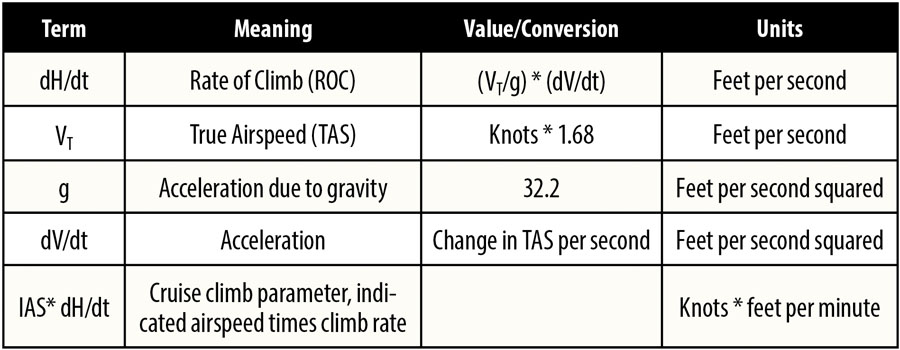
The calculated data begins with a column for time starting at zero and increments in 1-second steps. The curve fit TAS is calculated using the equation from the trend line equation from the “True Airspeed v Elapsed Time” graph where “y” is the TAS and “x” is the time. Convert TAS (knots) to VT (ft/sec) by multiplying by 1.68. “G” is the gravitational constant. By using a 1-second time interval, dV/dt (the rate of change of velocity with respect to time) is simply the current VT minus the previous VT. Calculate the climb rate dH/dt = (VT/g) * (dV/dt) * 60. Multiplying by 60 in this last step is necessary to convert feet per second into pilot friendly units of feet per minute. The last step is to convert TAS back to IAS because this is what you will be referring to on your airspeed indicator. From the EFIS recorded data under these test conditions, the last column shows IAS = TAS/1.10; use this relationship to calculate IAS. The last column is used to determine the cruise climb. It is the IAS multiplied by the dH/dt. Now you are ready to plot dH/dt versus IAS and IAS*dH/dt versus IAS.
dH/dT = (VT/g) * (dV/dt)
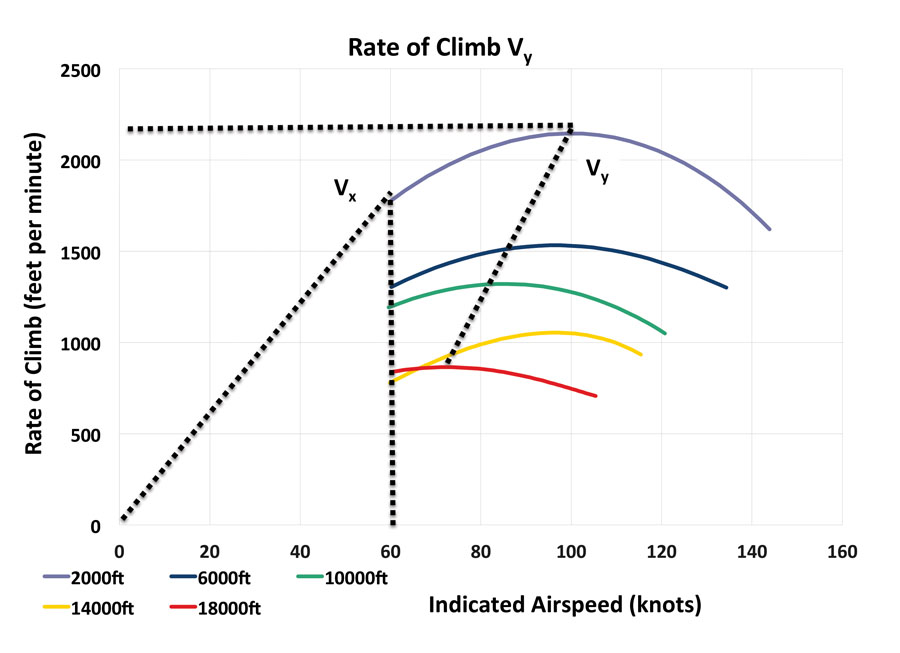
Best Angle of Climb Speed (VX)
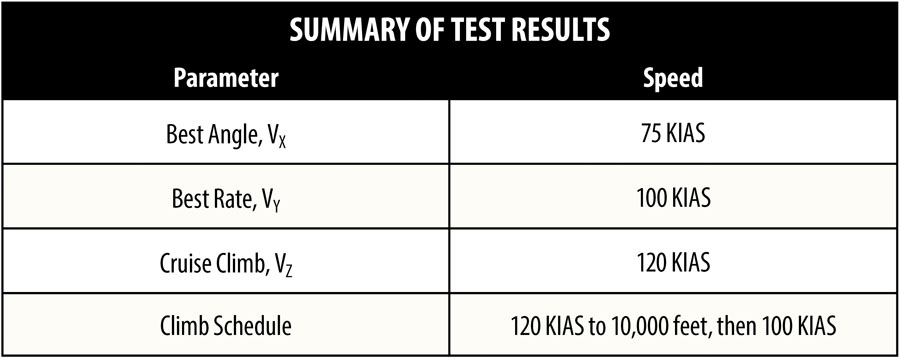
You can determine the speed for best angle of climb (VX) by drawing a tangent on the “Climb Rate v Airspeed” graph from the origin of the climb rate to the climb rate curve. Climbing at this speed will yield the greatest height gain per distance traveled. In straight-wing, propeller-driven aircraft, this speed tends to be just above the stall. In my RV-8, the best angle of climb is at 60 KIAS, which is also the power-off stall speed. My POH lists the VX as 75 KIAS. This slightly faster climb speed still results in a steep climb angle but has a decent margin to the stall. In this case there was no significant change in VX as altitude increased (the theory is that VX slowly increases with increasing altitude).
The most common use for VX is clearing obstacles during a short field takeoff. If you truly have obstacles to clear, VX is the best speed for the job. The disadvantages of climbing at VX are the small margin to stall speed, poor forward field of view with a high nose attitude, and poor engine cooling. In the event of an engine failure, the aircraft will decelerate quickly, making recovery challenging. Use VX if you must, but as soon as you are clear of obstacles, accelerate to VY or faster.
Best Rate of Climb Speed (VY)
The airspeed for best rate of climb VY is simply the peak or highest point of the climb rate on the “Climb Rate v Airspeed” chart. Climbing at this speed will yield the greatest height gain per minute. In my RV-8, VY is 100 KIAS at 2000 feet and reduces by around 1 knot per thousand feet. This is shown by the sloping line joining the peak of the climb curves at each altitude.
The most common use for VY is gaining height quickly immediately after takeoff. Climbing at VY results in higher stall margin, better field of view, better engine cooling, and easier recovery from an engine failure than VX.
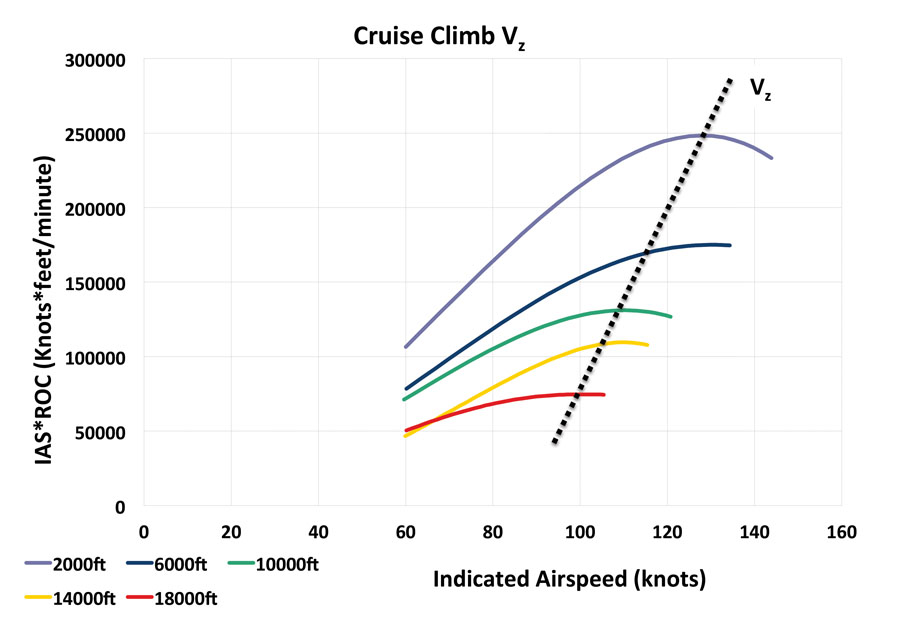
Best Efficiency of Climb or Cruise Climb Speed (VZ)
VX and VY are both maximum effort speeds; that is, they maximize a single parameter of performance. When flying cross-country, the climb rate (fpm) and the forward rate (knots) are both important. You want to get to altitude, but you want to get to the destination as well. If you multiply the climb rate by the airspeed and then plot the result against airspeed, the resulting curve looks like the climb rate curve but the peak is shifted right. If you climb at the airspeed where the fpm*knots is maximized, this can be defined as cruise climb (VZ). This idea is a play on Carson’s speed for cruise flight, which sought to maximize Velocity * L/D.
The term VZ was coined by Norm Howell in his master’s thesis titled “Introducing VZ: Best Efficiency Climb Speed for Small Airplanes.” VZ is a higher airspeed than VX or VY and results in a lower pitch attitude for better forward field of view, more comfort for passengers, better engine cooling, and easier recovery in the event of an engine failure. In a normal takeoff, I continuously accelerate from liftoff speed to achieve VZ at 1000 feet AGL. VZ in my RV-8 is 125 KIAS at 2000 feet and reduces by about 1 knot per thousand feet.
Don’t be Precisely Inaccurate
This discussion is aimed at the engineers in the audience. Once you have all your climb performance plotted, avoid the temptation to agonize over the exact speed for VX, VY, or VZ. One thing you will notice about the climb performance of RVs is the top of the curves are relatively flat. This means that over a wide speed range, there is only a small change in climb rate. This insensitivity is a good thing. It also means that writing VY = 83.47 knots in your POH is really no better than 80, 85, or 90 knots. Rather than being precise, pick a nice round easy-to-remember number that corresponds to a marking on your airspeed indicator. Airplanes tend to fly nicer at higher airspeeds than slower ones, so if you determine VY is 83.47 knots, round up to 85 rather than down to 80.
It is normal for VY to reduce a little with altitude. While it may be precise to say the best rate of climb speed reduces at 1 knot per 1000 feet in an RV-like aircraft, trying to fly that schedule precisely is overthinking the matter. Based on my climb test results, my normal climb schedule is as follows: 120 KIAS to 10,000 feet, then 100 KIAS above that.
Safety
The biggest risk with the level acceleration flight test technique is stalling at high power and low altitude. In general aviation aircraft, all the important speeds are between the stall and around twice the stall speed. So to get good data, you want to be as close to the stall as possible prior to leveling off and accelerating. Stalling with climb power tends to make the stall characteristics worse. The effects of the engine torque and spiraling slipstream are greatest, and ailerons are less effective due to the low speed. You will want to practice deliberately stalling and recovering in this configuration at altitude before you risk it happening closer to the ground.
Conclusion
The level acceleration method works well, but good results require a data acquisition system, smooth and accurate flying, and, last but not least, a little data reduction. The payoff is economically gathering a lot of data over a wide range of conditions.
















Hi Nigel, very interesting article. Quick question – how do you create the polynomial? Is it really needed if your EFIS is logging data at 1 Hz or better? Also, is the “climb angle and rate” graph correct on the website? The dotted lines seem to be in a strange place on the Vy line that should be vertical, I think. Thanks again for this shortcut!
Mickey – you need to calculate the coefficients of the polynomial because you must use those coefficients to calculate the curve fit TAS. This is independent of the EFIS data resolution. This smoothes out the errors in the initial readings and provides an idealized climb curve. You need to do this once for each altitude flown.
In Excel, use this formula to create the polynomial =LINEST($G$5:$G$132,$C$5:$C$132^{1,2,3,4},TRUE,FALSE)
In my case, the TAS values are in column G and the seconds since start of climb are in column C. Depending on the version of Excel you are using, you may need to enter this as an array formula across the 5 cells that will contain the 5 returned coefficients for the polynomial. This is what the results look like (spacing not correct here, the first row is the column headings):
Outputs x4 x3 x2 x1 c
Coefficients -5.6439E-07 0.000256003 -0.043885663 3.44616192 73.67792065
The formula above goes in the cells where you want the return values, the rest are just labels I entered.
Note that this is different from adding the polynomial trendline to the raw data plot. That is done by right-clicking the data series on the plot, selecting add trendline, and specifying a polynomial with an order of 4. You can choose to show the formula for this trendline on the graph, but I found that it is not displayed with enough precision for you to use it in calculating the curve fit TAS.
Like the use of Linest and adequate precision on the coefficients.
Awesome David – thanks for that. All clear – let me plug it into my test data to see what I get!
Hi Nigel, I read your very interesting article on KitPlanes. It was brought to my attention by a user of my software. I’m adding a level acceleration climb tool. After a bit more testing it will be released soon. I created a short video to demo to the user how it looks. No narration but it follows the steps in your article. You can view the video here: https://youtu.be/UOpnr-0crK0
It would be great to use some of your flight data in my acceptance tests. If that’s possible let me know.
Outstanding article and a very useful flight test technique. One possible correction: in the text description below the “Calculated Data” table, you mention that “‘G’ is the gravitational constant.” I think you meant to say that “g” is the acceleration due to gravity in feet per second squared, rather than referencing Newton/Einstein’s universal “Big G” constant. Looks like it’s correct in the “definition of terms” table. Just confused me for a second. Thanks again for the great article!
David Carter, You can actually increase number of decimals displayed in the equation for the trend line on the chart. In Excel 97, once equation is shown on the chart, right-click on the equation and select “Format Data Labels….”. The select Number, Number and increase to 6 (or more) decimal places.
For Excel chart novices, to add a trend line: right-click on one of the data points on the curve and “Add trend line”. Polynomial, increase order to 4 (or more). On the Options tab, check “Display equation on chart”.
Read this a while back, and it is a great one to read again. Love the approach to sifting the data and choosing operational speeds based on operational usability and safety (avoidance of precision in being inaccurate, ha ha..). Thanks again for the great write up!
I do not understand the need to start 500′ below desired altitude. By the time I reach the desired altitude, airspeed has already increased to way above stall speed. I find it easier to slow plane down to near stall at desired altitude and then add full throttle while looking at VSI to maintain altitude.
With my Dynon D100 EFIS I can display TAS. I’m thinking that determining and using TAS rather than IAS will be more versatile — valid for all density altitudes?
But certainly this is a much faster method to determine Vx, Vy and Vz. Better engine cooling too!
If there is interest, I’d be happy to share the tips and tricks I used to rapidly put the equation in the “Curve fit TAS” column in the Excel spreadsheet. Very fast even with 6th order equation with 10 digit display accuracy.
I would like the entire data file so I can run with the whole thing and check against your calc.
I find it disturbing that you are showing varying precision of the coefficients. The t^4 coefficient shows up with one significant digit. I would like to see a lot more than one digit for coefficients. Perhaps use scientific notation to five digits and get all coefficients to the same precision?
While smoothing the data by doing a curve fit is a good idea, I wondered about doing total energy change. A quick check of the published 10 seconds shows the potential energy change in one time step to be as big as 20% of the kinetic energy change. I suspect that including both velocity change and height change MIGHT make for a better fit, but I would need the entire data set to take a cut at that.
Once we have the accel curve fit equation, we can differentiate it once to get accel directly. Why not? We can also get the Vx term directly by differentiating the accel curve and picking the max point. We can also plot the data in smaller increments in an attempt at picking off speeds at 1 or 2 knot increments instead of surrendering to a one second increment.