Proper selection and design of the propeller is one of the keys to airplane performance. A reciprocating engine that powers an airplane delivers its power by rotating a shaft. In order to provide thrust, the torque the engine exerts on its crankshaft must be converted to a reaction against the air. That is the job of the propeller. The more efficiently the propeller converts shaft horsepower to thrust, the better.
Momentum: The Actuator Disk Theory
All aircraft propulsion systems work on the principle of action and reaction. They accelerate air (or some other combination of gases) backwards, generating an equal and opposite forward reaction force. As the air is accelerated aft, its momentum is increased. Thrust is the result of the change in the momentum of the air induced by the propulsion system.
Although there are many intricacies to propeller design, which we will discuss in the future, the whole purpose of the propeller and its rotating blades is to accelerate air aft to generate thrust. Before we dive into details, lets take a look at the fundamentals of the stream tube of air affected by the prop.
The simplest approach is to treat the propeller as an “actuator disk.” The actuator disk is an idealized model of a propeller, consisting of an imaginary disk having the same diameter as the propeller. The air passing through the disk is assumed to undergo an instantaneous, uniform change in velocity. This is a simplification, of course. In the real world, the velocity change happens as the air flows over the prop blades and is not instantaneous.
Actuator disk theory ignores all of the details of the propeller blades, engine, rpm, etc. It is a pure energy and momentum balance approach to the problem. The efficiency predicted by actuator disk theory is a theoretical maximum for a given diameter, power, density altitude, and airspeed. While real propellers never quite achieve this, some come remarkably close. The real value of actuator disk theory is that it lets us examine the effect of propeller diameter, thrust, and forward velocity on propulsive efficiency.
Actuator Disk Equations
The thrust produced by an actuator disk is given by:
T = 2 A ρ v (V+v) ; (eq. 1)
where:
A = area of the actuator disk
ρ = density of the air
V = free stream airspeed
v = change of airspeed as air passes through the actuator disk.
The power which must be input to the actuator disk to generate thrust (T) is the product of thrust times the velocity of the air as it passes through the disk (V + v):
Pin = T (V + v) ; (eq. 2)
The power output of the propeller to the airplane is the product of the thrust times the free stream velocity:
Pout = T V ; (eq. 3)
The ideal propeller efficiency is the ratio of power out to power in. When all of the algebra is done we are left with:
propeller efficiency (η) = V / (V + v) ; (eq. 4)
We can use these equations to determine the ideal efficiency of a propeller. The most interesting observations come from the equations for thrust and efficiency.
First, lets look at equation 1, which describes the relationship between thrust (T), disk area (A), airspeed (V), and velocity change across the disk (v).
At constant thrust, if the propeller diameter gets larger (bigger A), the velocity change across the disk (v) gets smaller. We can get the same thrust by either producing a large velocity change across a small disk or a small velocity change across a large disk.
Since a propeller produces thrust by changing the momentum of the air passing through the propeller disk, to get a fixed amount of thrust, the propeller must add a fixed amount of momentum to the air-per-unit time.
The mass of air going through the disk is determined by the airspeed (V) and the area of the disk.
The momentum added to the air is the product of the mass of air passing through the disk multiplied by the change in speed (v) going through the prop. The larger the mass flux through the disk, the smaller the velocity change (v) for a given thrust.
We can get the same result by accelerating a large mass of air a little bit or a small mass of air a lot. This is critically important to the efficiency of the propeller.
Diameter Effects
To see the importance of this relationship between propeller diameter and air velocity change across the propeller, we turn to equation 4: efficiency.
The first thing we see is that the velocity change across the propeller (v) is in the denominator. This means that as (v) gets larger, the propeller efficiency drops. Conversely, as (v) gets smaller propeller efficiency increases. In the limiting case where the velocity change across the prop goes to zero, the efficiency equals one.
The reason for this is that while thrust is a result of the change in momentum of the air, power required is a function of the change in kinetic energy. Change in momentum is proportional to velocity change. Change in kinetic energy is proportional to velocity change squared. The squared relationship means that kinetic energy input (and hence power input) rises faster than momentum change as (v) increases.
To minimize the kinetic energy change for a given momentum change, we want to impose a small velocity change on a large mass of air.
Airspeed Effects
Notice that as airspeed (V) increases, the efficiency for a constant velocity change across the propeller (v) also increases. If airspeed were to get infinitely large, the efficiency would again go asymptotically to 1.0.
This is because the mass flux through the propeller (which is the mass the prop acts on to generate thrust) is the product of the propeller disc area (A), the air density (ρ), and the airspeed (V). As airspeed increases, the mass flux through the prop increases, so the amount of velocity change (v) across the prop needed for a constant thrust drops linearly with increasing airspeed.
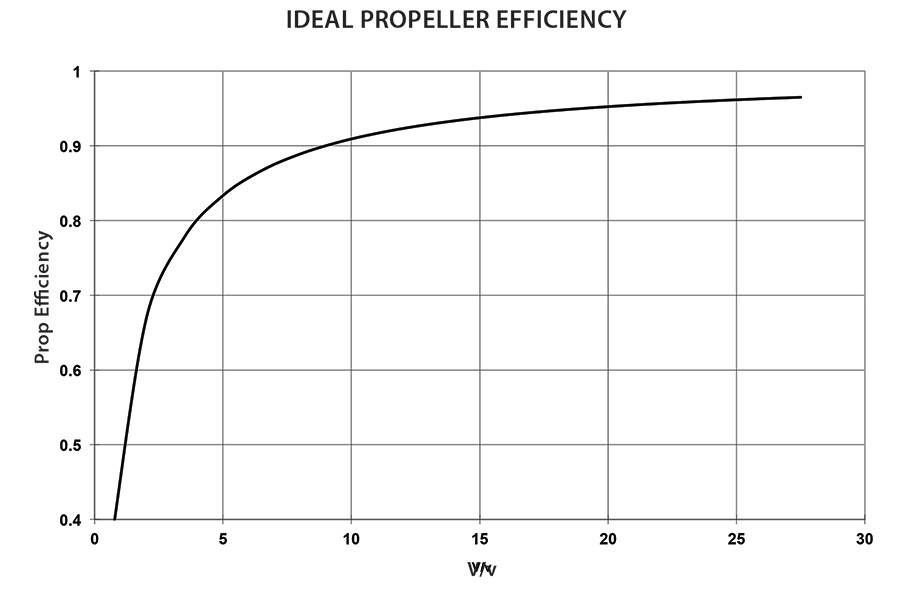
The critical parameter determining ideal propeller efficiency is the ratio of the airspeed to the velocity change across the propeller: (V/v). The effect of this speed ratio on ideal efficiency is plotted in Figure 1. A look at this plot can begin to give us some insight into the effects of propeller size. Note that the ideal efficiency goes above 90% at a (V/v) of about 9. For values above about 15, there is very little gain in ideal efficiency as (V/v) increases further.
Figure 1: The critical parameter determining ideal propeller efficiency is the ratio of the airspeed to the velocity change across the propeller: (V/v). Note that the ideal efficiency goes above 90% at a (V/v) of about 9. For values above about 15, there is very little gain in ideal efficiency as (V/v) increases further.
This tells us that there is a point of diminishing returns as we increase prop diameter. Above a certain size, increasing diameter does not help ideal efficiency much, while the increasing weight and parasite losses of a real-world propeller make any further increase in diameter ineffective at improving performance. The goal of the designer is to design to the right of the “knee” of the efficiency curve while still keeping the propeller diameter reasonable.
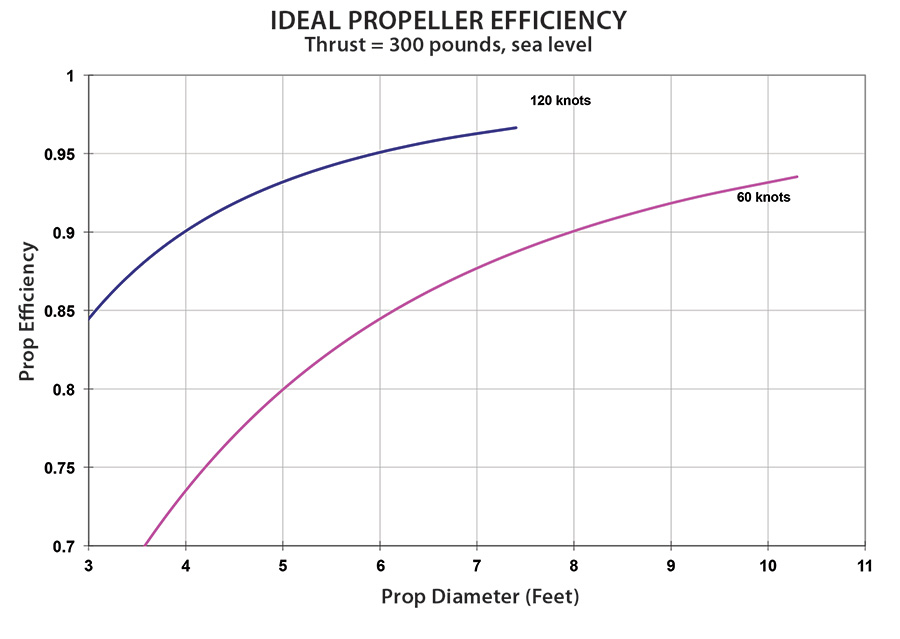
This phenomenon gets more important at lower airspeeds speeds. Figure 2 shows the effect of propeller diameter on ideal propeller efficiency for a propeller developing 300 pounds of thrust at sea level. The two curves are for different airspeeds.
Figure 2: The effect of propeller diameter on ideal propeller efficiency for a propeller developing 300 pounds of thrust at sea level. The two curves are for different airspeeds. The ideal efficiency of the 4-foot diameter propeller has dropped from 90% at 120 knots to about 73% at 60 knots.
First look at the upper curve, for a propeller operating at 120 knots airspeed. Notice that by the time the propeller diameter is up to 4 feet (48 inches), the ideal prop efficiency is at about 90%. As diameter increases, the ideal efficiency also increases, but there is not a lot of improvement available once diameter gets much above 6 feet (72 inches).
The situation changes dramatically at lower airspeed. The second curve is for a propeller developing the same 300 pounds of thrust at an airspeed of 60 knots.
The ideal efficiency of the 4-foot diameter propeller has dropped from 90% at 120 knots to about 73% at 60 knots. As diameter increases above 4 feet, the ideal efficiency continues to increase rapidly. We have to get to a diameter of about 8-1/2 feet before we get to 90% ideal efficiency.
Different Props for Different Planes
The effect of airspeed and propeller diameter on the efficiency of the propeller helps explain why different types of propellers are used on different types of airplanes.
For fast airplanes, a relatively small diameter propeller will give reasonably high cruise efficiencies. The propeller diameter chosen is a compromise between climb and cruise performance, but it tends to lean toward the cruise side.
For airplanes that fly slowly, there is a much greater incentive to increase propeller diameter. Ultralights are a good example of this. Early ultralights, such as John Moody’s original Easy Riser, used direct-drive propellers attached to the crankshaft and turned at engine rpm. The engines used were high-revving 2-strokes, so early ultralights had very small propellers turning at very high rpm.
They also flew very slowly. This combination made for very poor efficiency and very little actual thrust coming from the propeller. The early direct-drive ultralights were just barely capable of achieving a positive rate of climb if everything was just right. I remember watching foot-launched ultralights attempt to take off early one morning at Oshkosh ’78. A few made it into the air, but a lot made a series of hops and skips across the field like overfed pelicans without getting airborne for any sustained period.
The development of reduction drives changed everything. Instead of a 40-inch diameter propeller turning 6000 rpm, it was now possible to use a 70-inch diameter propeller turning 2500 rpm. This produced an enormous improvement in takeoff and climb performance. A modern ultralight can take off in a very short distance and climb at an impressive angle.
Human-powered and solar-powered airplanes are other classes of machines that need very large propeller diameters. They fly even more slowly than ultralights, and are also cursed with the lowest power-to-weight ratios of any heavier-than-air flying machine. A typical human-powered airplane has only 2% to 3% of the power-to-weight ratio of a Cessna 150. Clearly it needs to use every bit of its meager power as efficiently as possible. To make it work at all, an extremely large-diameter, slow-turning propeller is needed.
Next time we will turn our attention to the blades themselves, and begin to explore some of the phenomena that are important in the detail design of a propeller.