
For a lot of typical private flying, planes like the Sling 2 LSA offer an effective combination of performance and price. (Photo: Kevin Wing)
Last month we took a look at how the required cruise speed affects the cost and complexity of the airplane. As cruise speed increases, the airplane requires more power, burns more fuel, and becomes more complex as retractable landing gear, high lift systems, and constant-speed propellers become necessary to provide the required performance.
With this in mind, when we are setting our design requirements, it’s important to ask the question, “How fast do we really need (want) this airplane to go?”
We usually look at cruise speed in the context of flying cross-country. Unless the airplane is intended for racing or to set an absolute record, sheer speed in and of itself has little value. What is important is how fast we need to fly to get from A to B effectively.

Figure 1: For very short trips, the time en route isn’t all that different for fast and slow planes. But for long trips, the difference is significant.
Speed and Range
How fast we need to fly is a direct function of how far we want to go. The faster the airplane is, the farther it can go in a given time. For most pilots, cruise speed defines the useful radius of action of the airplane. This is particularly true for private pilots since much of our flying consists of single-day out-and-back excursions.
With this in mind, let’s take a look at how cruise speed affects time and distance.
Figure 1 shows distance vs. time for several values of cruise speed for ranges up to 200 miles in zero wind. For this example, the airplane first climbs to cruising attitude at 70% of cruise speed and then cruises at constant speed thereafter. All of the airplanes have the same rate of climb and cruise at the same attitude. Note also that speed is in knots, but distance over the ground is shown in statute miles.
Let’s look first at the time to cover 100 miles, which is a common day-trip radius of action. Our slowest (60-knot) airplane takes 90 minutes to do this trip. Increasing speed to 80 knots (Cessna 150-ish speed) reduces this to 68 minutes. Moving up to the Light-Sport maximum cruise speed of 120 knots cuts this trip to 46 minutes.
For this short range, as we get faster than this we begin to hit diminishing returns, particularly if we take into account the time to fly the traffic pattern and taxi in. Going from 120 knots to 160 knots only saves about 10 minutes. This means that if they take off simultaneously, the 120-knot airplane will be entering the downwind at about the same time that the 160-knot airplane arrives at the destination airport ramp. A further increase to 200 knots only saves an additional 6 minutes.
Moving out to a 200-mile radius, the first thing we can see is that the trip in the 60-knot airplane is now a 3-hour evolution. Our 80-knot machine gets us there in about 2 hours and 15 minutes. Our Light Sport (120-knot) ride does this mission in 1.5 hours. At this range, the 160 knot airplane reduces travel time by 22 minutes over the Light Sport, which might start to look worthwhile to some pilots. Even at 200 miles, the benefit of increasing speed to 200 knots is relatively small.
At longer ranges, additional speed begins to pay off. At 450 miles, which is about the maximum range of many single-engine airplanes, going fast starts to be much more desirable. At this range, the 60-knot airplane is a complete non-starter. The 80-knot airplane can do the mission, but it takes 5 hours. While this is doable, if tedious, for a one-way trip, it means that there is no reasonable chance of a same-day out-and-back excursion.
The 120-knot airplane takes 3 hours and 20 minutes to do the 450 miles. This is long enough to be a significant undertaking, but within the limits of what most pilots would be willing to undertake at least occasionally.
Moving up to 160 knots shaves almost an hour off the 450-mile mission, bringing the time down to 2.5 hours, while a 200 knot cruise reduces the mission time to 2 hours.
At this range, the faster cruise speeds provide a very desirable improvement in mission performance.
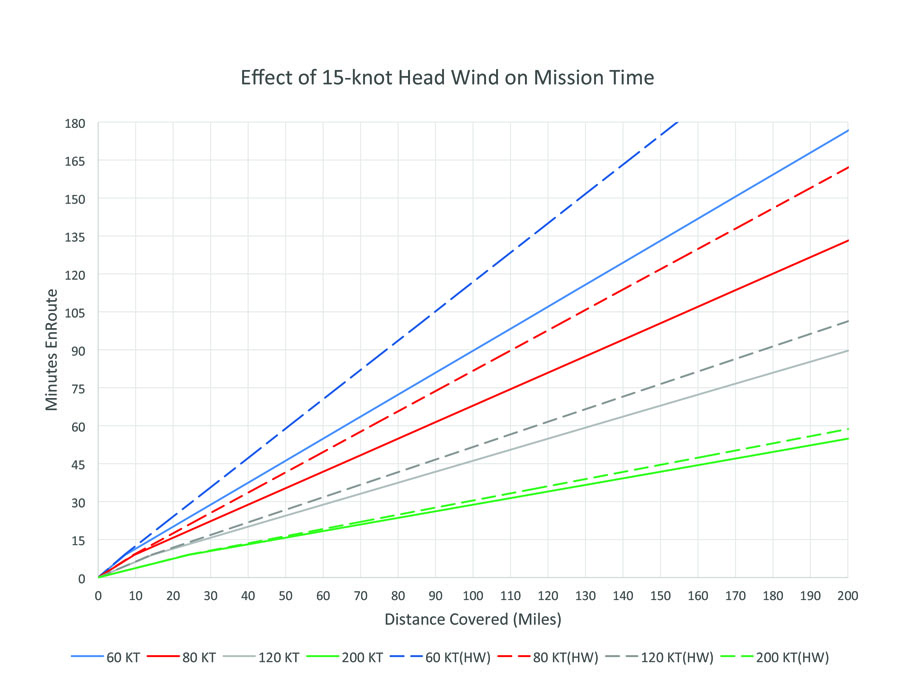
The slower the airplane flies, the more a given headwind increases mission time. In these examples, solid lines represent zero wind and dashed lines represent flying into a 15-knot headwind.
Wind
So far, we have only looked at zero-wind conditions. Unfortunately, the wind is rarely zero and many flights are into a significant headwind that reduces the airplane’s speed over the ground.
The slower the airplane flies, the more a given headwind increases mission time. This effect is nonlinear because a given wind speed is a greater percentage of a slower cruise speed than of a faster cruise speed. For example, a 15-knot headwind reduces the over-the-ground speed of a 60-knot airplane by 25%, while the same wind causes a 12.5% penalty for a 120-knot airplane, and a 7.5% penalty for a 200-knot airplane. For the faster airplane, the wind costs a smaller percentage of the already-shorter zero-wind mission. Accordingly, a given headwind will increase the flight time much more for a slower airplane than a faster one, and this penalty will rise rapidly with slower cruise speed.
This effect is illustrated in Figure 2. For each cruise speed, the solid line represents the zero-wind case, while the dashed line represents flying into a 15-knot headwind.
On our 100-mile day excursion, the 15-knot headwind increases the mission time for the 60-knot airplane by 25 minutes. The penalty for the 80-knot airplane is about 15 minutes, while the 120-knot airplane is only delayed by about 5 minutes, and the delay for the 200-knot airplane is very small indeed.
As the range increases, so does the time penalty for the headwind. If mission requirements for the airplane include routinely flying against significant winds, the range at which flying faster begins to pay off is shorter than it is for the zero-wind case.

With retractable gear, constant-speed props, and cruise speeds in the 200-knot range, the Velocity V-Twin was designed for long cross-countries. (Photo: Richard VanderMeulen)
A Few Conclusions
From the above, we can begin to see some natural breakpoints for our specified cruise speed. The first of these is that if the airplane is slower than about 80 knots, its cross-country capability is minimal. It’s suitable for local, recreational flying only.
80 knots seems to be about the lower end of the range of cruise speed for useful cross-country capability, but increasing speed to about 120 knots yields a meaningful improvement for day excursions. The 120-knot airplane has a significantly larger radius of operation for single-day VFR out-and-back flying.
It’s only when the required range gets significantly above 200 miles that increasing cruise speed beyond the Light Sport limit of 120 knots really begins to pay off.
Looking at the conclusions above, it’s not surprising that a large number of popular types have cruise speeds that fall in the 80- to 120-knot range. In fact, the certified airplane types that have sold the most units in history essentially all fall in this performance band.
This also makes sense from a cost-effectiveness viewpoint. This speed range is where an airplane with fixed landing gear and a fixed-pitch propeller works well. Cost is a major concern for most private pilots. The fixed-gear, fixed-pitch airplane costs less to buy, less to maintain, and probably burns less fuel than a higher powered retractable with a constant-speed propeller. Given the minimal time value of higher cruise speed for a lot of typical private flying, these airplanes offer the most cost-effective combination of performance and price for many aviators.
It also shows that the 120-knot maximum speed specified in the U.S. Light Sport rules is a sensible choice. It’s a speed that is achievable by simple airplanes that can be safely operated by Sport Pilots, which is also fast enough to make the airplanes effective for the kind of flying the majority of Sport Pilots do.
Finally, as attractive as the idea of a really fast airplane is, the added cost and complexity required to get that alluring top speed is only really useful to the pilot if the airplane will be used primarily for longer range cross-country travel.

![]()
Barnaby Wainfan is a principal aerodynamics engineer for Northrop Grumman’s Advanced Design organization. A private pilot with single engine and glider ratings, Barnaby has been involved in the design of unconventional airplanes including canards, joined wings, flying wings and some too strange to fall into any known category.














Is there a case for aircraft encountering more headwinds than tailwinds? Measured I suppose by wind speed times duration in time? If headwinds and tailwinds are equally encountered, what would the dynamic of adverse winds be that would increase the attractiveness of faster planes?