Nondimensional quantities allow for analysis of data independent of an objects physical dimensions, which makes relevant comparisons between objects easier. In aerodynamics, the most common nondimensional quantities are force and moment coefficients.
The goal of an aerodynamic test or analysis is to define the fundamental characteristics of a configuration. The raw results of aerodynamic testing are dependent partly on the geometry of the configuration and partly on the dimensions of the test article. These dimensions include physical size, airspeed, weight and air density among others. This size dependence makes it difficult to compare the results of different tests on the basis of raw forces. If one wing produced 100 pounds of lift when tested, and another produced 150 pounds, what does it mean? It could be because the airspeed was higher in one test, or that one wing was bigger than the other, or one wing may have had a higher-lift airfoil.
Another problem arises because people use different systems of physical units. In the U.S., for example, we use slugs, pounds and feet as our units of mass, force and length, respectively, while most of the rest of the world uses kilograms, newtons and meters. To avoid confusion over units, it would be desirable to put data in a form where the same number has the same meaning regardless of the system of physical units being used. A person working in the metric system should get the same answer as someone who is working in English units.
To be useful to the designer, the test data must not only give raw force, but also describe the fundamental characteristics of the configuration. It should be equally applicable to a small wind-tunnel model or a full-size airplane. This provides a basis for applying test data to predict the characteristics of the real airplane and makes it possible to realistically compare the results of multiple tests.
These concerns have led to the use of nondimensional quantities. A nondimensional quantity has no measurement units such as pounds, feet, etc. It is independent of the physical dimensions of the object or the phenomenon it describes. Through proper analysis of data, it is possible to put it in nondimensional terms, thus removing the size and unit dependence that make comparisons difficult from the result. The most commonly known nondimensional quantities in aerodynamics are the force and moment coefficients.
Lift Coefficient (CL)
The lift coefficient is a measurement of how much lift a given shape will generate. It is determined by the geometry of the configuration (shape and angle of attack) rather than how big it is or the airspeed. We will use the lift coefficient as an example of how nondimensional quantities are generated and used.
Suppose we conduct a wind-tunnel test of a model of an airplane. When we are done we know how much lift the model generated at each angle of attack tested. We also know the dimensions of the model, the airspeed at which we tested and the density of the air in the wind tunnel.
The lift we have measured has units of pounds force (for those of us in the U.S.). This value of raw lift is a function of the size of the model, airspeed and air density as well as shape and angle of attack. We want to reduce this data to a table of lift coefficient versus angle of attack, which is independent of size, airspeed and air density.
The first step in nondimensionalizing the lift removes the influence of the size of the model. We convert the data into units of pounds of lift per square foot of lifting area by dividing the lift (in pounds) by the wing area (in square feet), yielding a quantity with units of pounds per square foot.
The wing area is called the reference area for the lift coefficient. The proper definition of reference area is important, and confusion in this area has caused many errors. It is possible to use any area for a reference and derive a lift coefficient. The potential problem arises when we try to use that data later on. For the data to be useful, we must know what reference area was used to reduce the data and how to derive an appropriate reference area to use when applying the data to a model or airplane of a different size. For this reason, reference area is almost always an area that is both easily measurable and clearly defined by the geometry of the airplane.
For most airplanes the reference area for aerodynamic force coefficients is the wing area, which comprises the exposed area of the wing and the area of that portion of the wing that would be inside the fuselage if the leading and trailing edges were extrapolated to the airplane centerline.
For complex wing planforms people sometimes use a simplified geometry to define a reference area that is not the true wing area. While there is nothing fundamentally wrong with this procedure, it adds an element of potential confusion, and one must be careful to make sure that how the reference area is to be derived is well documented. Non-standard reference areas can also make results misleading, as they ignore part of the wing area, and may thus ignore some important configuration effects on aerodynamics.
Before our digression into the pitfalls of reference area, we had reduced our raw lift data to units of lift per unit area, thus making it independent of the physical size of the airplane. This seems to solve our size-dependence problem. As long as we know lift per square foot, all we need to do is multiply by wing area to get the lift. The problem is that our lift per square foot applies only to the specific airspeed and air density of our original test.
To remove the effects of airspeed and atmospheric conditions from the data we must divide lift per square foot by a quantity that characterizes the effects of both airspeed and air density on the aerodynamic forces generated by the model.
The quantity we use is dynamic pressure and is symbolized in equations by the letter Q. The dynamic pressure is a measure of the kinetic energy in the airstream, and it determines how much force the airstream can exert on an object.
If we allow the airflow to run into a wall that brings it to a halt, the pressure of the air rises as the kinetic energy of moving air is converted to potential energy in the form of increased pressure. The difference between the stagnation pressure, which is the total pressure of the air at a stagnation point where the airstream is brought to a halt by an obstacle, and the static pressure, which is the pressure in the undisturbed free stream, is the dynamic pressure. The dynamic pressure is a measure of the ability of air, having a given density and airspeed, to exert aerodynamic force on an object; it is the appropriate quantity to use in reducing our aerodynamic force data.
Note that in dividing our original lift data by reference area, we came up with a quantity that had units of pounds per square foot (or newtons per square meter for you metric types). Dynamic pressure also has units of force per unit area, so when we divide lift per unit area by dynamic pressure, the units in the numerator and denominator cancel, and we are left with a pure number with no physical units. This number, called the lift coefficient, is nondimensional. It is the same for a given airplane shape and angle of attack regardless of the size of the airplane, the density of the air or the airspeed. (This is not completely true because Mach number and Reynolds number get into the picture, as we will see later; but to the first order it is correct.) The beauty is that the plot of lift coefficient versus angle of attack lets us determine the lift of the airplane at any airspeed and for any size airplane or model of the same configuration.
The data we took from our wind-tunnel model can be applied directly to the full-size airplane, and the lift characteristics of different airplanes can be compared directly. The lift at a given angle of attack, airspeed and air density can be calculated by multiplying the lift coefficient at that angle of attack by the wing area and the dynamic pressure. Equations for all of these quantities follow:
CL = L/(SQ)
where:
L = Lift
S = Wing area
Q = Dynamic pressureQ = 1/2 ρ V2
where:
V = Airspeed
ρ = Air density
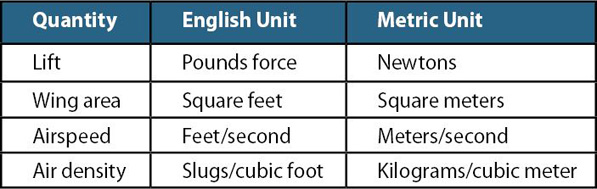
Note: It is essential that all of these quantities be measured in a consistent set of units. The proper units are shown in the accompanying table.
Drag Coefficient (CD)
Drag data is reduced to coefficient form the same way as lift data is. For a complete airplane, the only difference is that the aerodynamic force we start with is drag instead of lift. The reference area is still the wing area, and the dynamic pressure is the same.
For individual non-lifting components such as bodies, struts, wheels, etc., the reference area for the drag coefficient is usually the frontal area of the component. This is another place where reference area can get a careless worker into trouble.
Suppose, for example, that we want to determine the effect of a fixed landing gear wheel on the overall drag coefficient of an airplane. There is test data available from several sources giving the drag coefficients of wheels. It appears simple to add the drag coefficient of the wheel to the drag coefficient of the airplane. Unfortunately, the CD of the wheel uses the frontal area of the wheel as reference area, while that of the airplane uses the wing area. Simply adding the two together will produce an incorrect result because they were nondimensionalized using different reference areas.
Before we can add the CD of the wheel to that of the airplane, we must convert it to the airplane reference area. This is done by multiplying by the old reference area (wheel frontal area) and then dividing by the new reference area (in this case the airplane wing area). Once the CD is based on the same reference area as that of the airplane, the two can be added together.
Pitching-MomentCoefficient (CM)
In addition to lift and drag, the airflow over the airplane also produces pitching moment. Pitching moment is nondimensionalized the same way as lift and drag are except for one difference. A moment has units of force times distance rather than simply force, as is the case for lift and drag. We therefore need to divide the moment by a characteristic length as well as by reference area and dynamic pressure. The reference length used is the mean aerodynamic chord (MAC) of the wing.
CM = M/(SQC)
where:
M = Pitching moment
C = Wing mean aerodynamic chord
The three aerodynamic coefficients we have just described are the fundamental quantities used to characterize the longitudinal aerodynamic characteristics of an airplane. They are universally used, and mean the same thing to all engineers regardless of the language they speak, or the system of physical units they use.