As we have been discussing for the past two months, it is quite common for stall speed requirements to drive the wing of an airplane to be larger than up-and-away performance optimization would suggest. We have already looked at how stall speed affects takeoff performance and how certification stall-speed regulations can affect wing size. It’s worth noting in passing that, even though homebuilders are not constrained by the FAR requirements, these requirements generally stem from good safety-related considerations.
Continuing along that theme, we now turn our attention to the effects of stall speed on the end of the flight. The two factors we must consider are landing distance (in a normal landing) and safety (in an emergency situation).
Landing Distance
Once the airplane touches down, it must come to a stop. How much distance this takes is a function of how fast the airplane is going. Touchdown speed, in turn, is a function of the stall speed of the airplane in its approach configuration. FAR Part 23 specifies approach speed as 1.3 VSO. Typically, “over the fence” speed is a bit below this, and the airplane decelerates a little during the flare. Accordingly, touchdown speed will be somewhere between 1.3 VSO and 1.0 VSO.
After touchdown, the brakes are capable of generating a given deceleration. This is limited by the capacity of the brakes to absorb energy and the traction between the wheels and the runway surface. This limit is not a characteristic of the aerodynamics of the airplane, so to the first order, the deceleration available from the brakes is independent of the approach speed. Accordingly, the roll required to come to a halt will be proportional to the square of the touchdown speed.
Accurate calculation of landing distance is complex since it is dependent on the details of the airplane configuration, runway conditions, brakes, tires, engine residual thrust, etc. This level of detail is beyond what is useful for preliminary sizing and certainly beyond what I can cover here.
Fortunately, for initial sizing purposes, we can use a simple equation generated by a statistical analysis of FAR Part 23 certified airplanes. A good approximation of landing roll on a smooth, dry, level, paved runaway is given by:
SLg = 0.265 VSO2
Where:
SLg = Landing roll in feet
VSO = Approach configuration stall speed in knots
(Source: “Airplane Aerodynamics and Performance,” Jan Roskam and Edward Lan, eq 10.100, p 494)
Figure 1: As stall speed increases, landing roll increases, too.
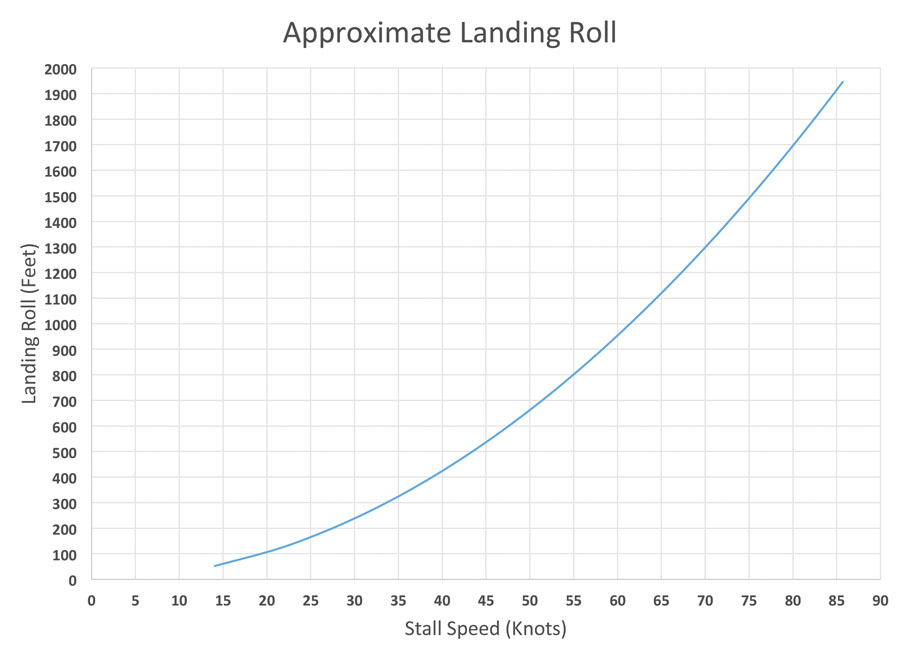
Figure 1 shows a plot of the landing roll as a function of stall speed as calculated by the equation above. The plot clearly shows the quadratic behavior of landing roll with stall speed. Looking, for example, at the FAR Part 103-mandated 24-knot stall speed, we see a landing roll of about 150 feet. At the Light Sport (LSA) stall speed of 45 knots, landing roll is up to approximately 550 feet. At the maximum VSO allowed by FAR Part 23 for most single-engine airplanes (61 knots), landing roll is up to about 1000 feet. Although homebuilts are not required to meet any of the certification standards, this should serve as a strong indication of the consequences of higher stall speeds on runway requirements.
Figure 2: Landing distance as a function of wing loading for three values of CLmax.
The impact of this effect on wing sizing is shown in Figure 2.
At sea level, standard day conditions, the stall speed of an airplane is given by:
Vstall (knots) = 17.194 * SQRT {(W/S) x (1/CLmax)}
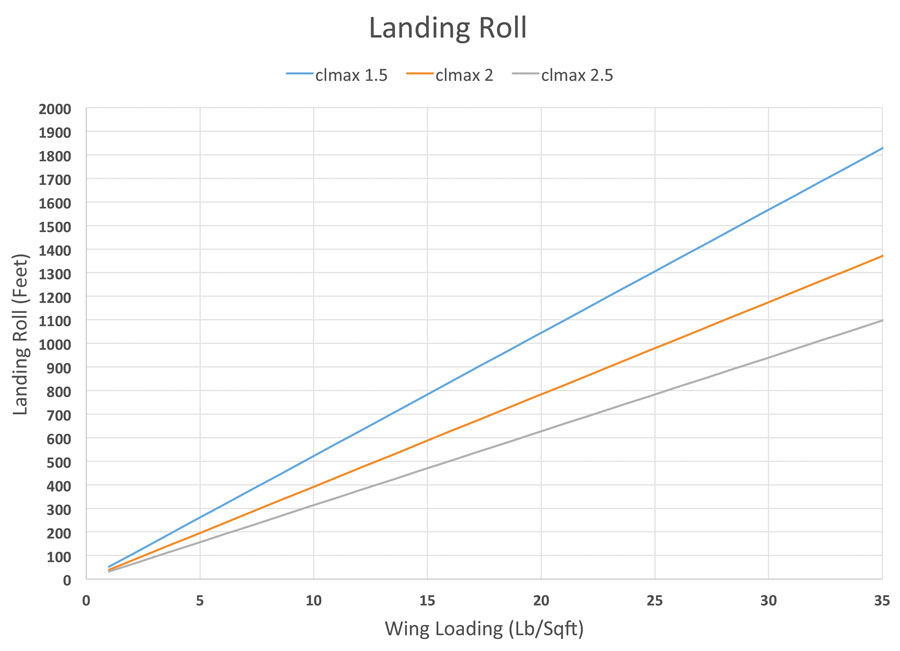
Notice that stall speed is proportional to the square root of wing loading (W/S). Since landing roll is proportional to stall speed squared, these two variations lead to the conclusion that landing roll is linearly proportional to wing loading. This behavior is illustrated in figure 2. The figure shows landing distance as a function of wing loading for three values of CLmax, which represent the effect of different types of high-lift systems.
Looking at typical wing loadings, we can see that at about 3 pounds per square foot, (ultralight) landing distances range approximately between 100 and 150 feet. With a Cessna 150-like wing loading (10 pounds per square foot), we are looking at a landing roll that ranges between about 300 and 500 feet, and at 20 pounds per square foot, landing roll ranges between 600 and 1000 feet. Wing loadings higher than 20 pounds per square foot are rare on single-engine airplanes, and this is one of the reasons why.
Safety
It is a sad fact that not every meeting between an airplane and the ground is a safe, routine landing. While we cannot design for every eventuality, it is highly desirable for the occupants of the airplane to have a reasonable chance of survival in the event of a forced landing or a mishap involving running off the runway during an attempted takeoff or landing.
Survivability in an accident is determined primarily by the deceleration loads placed on the airplane structure and occupants as the airplane impacts the ground. These forces are determined by the combination of the speed at impact and the angle of the velocity vector relative to the ground (or obstacle) on impact. The shallower the angle and the slower the speed, the greater the chance of survival.
Figure 3: As stall speed and impact angle increase, crash survivability decreases.
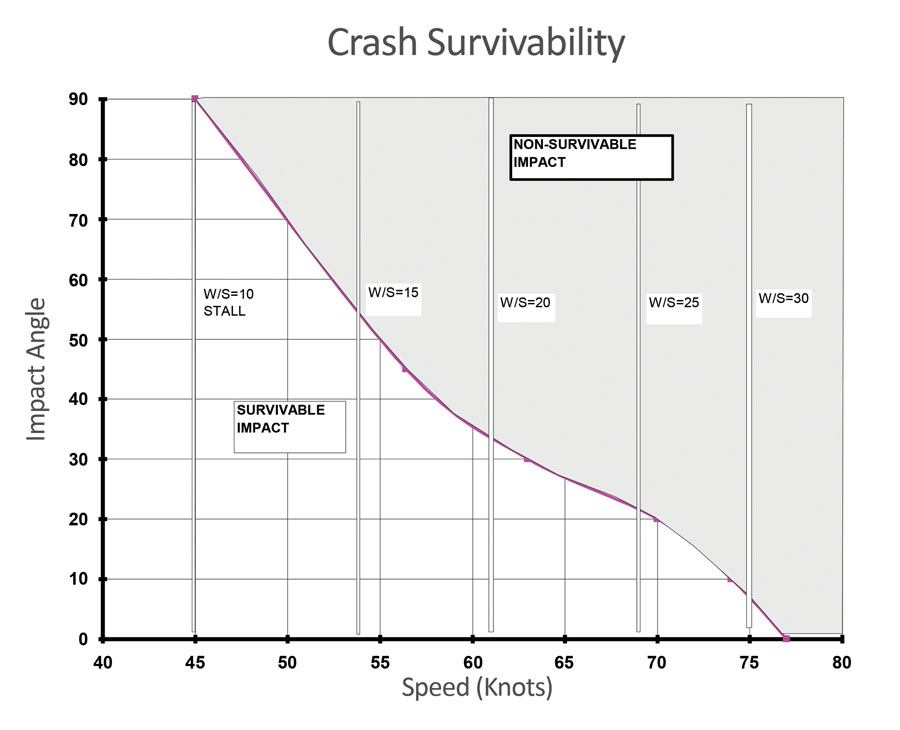
Figure 3 shows a plot of the survivable threshold of impact angle as a function of impact speed derived from SAE data on general aviation crash events.
Looking at Figure 3, we can once again see the effect of speed, and to some extent the reasons for certain regulatory limits.
Notice first that at the LSA stall speed of 45 knots, almost any impact that is not vertical is survivable. As long as the pilot maintains control and does not dive into the ground, an incident is likely to be survivable. At the FAR Part 23 single-engine stall speed limit of 61 knots, the critical impact angle is about 35 degrees. Once again, even allowing for the pilot keeping some margin of airspeed above stall, any reasonably controlled impact is likely to be survivable as long as the airplane does not collide with an obstacle.
Notice finally, that an uncontrolled arrival at any speed above about 76 knots is likely to be fatal.
The vertical bars on the figure show the stall speeds for several wing loadings at a typical value of CLmax. This also adds some understanding as to why light airplanes rarely have wing loadings greater than about 20 to 25 pounds per square foot. If we accept that a forced landing will occur at slightly above stall speed even with good piloting technique, we can see that as W/S increases above 25 pounds per square foot, the margin for error gets very small, and by slightly above 30 pounds per square foot, any flight that does not end in a controlled landing on a runway or other smooth, flat surface is likely to have an unhappy end.
With all of the considerations we have been discussing for the past few months in mind, the designer can now choose a wing size for the airplane.
Next month, we will turn our attention to the next critical configuration concern: balance.
