The author’s RV-3B right wing being assembled. The leading edge section is a torque-carrying structure, as will be the main section once the skins are all on. The result is a stiff two-cell structure.
Things twist. You can count on it, even if it’s not an election year. Some things twist because we want them to, and some things need to be prevented from twisting very far. Sometimes, such as with torque tubes, they deflect because it’s just their nature. Let’s look at that.
Twist is the deflection that happens when torque is applied to a structural member that has some length. Torque is simply another word for moment, in this case one whose axis of twist is parallel to the structure that resists the twisting. Any moment, whether it’s a torque or a bending moment, is by definition a force times a distance.
Torque tubes aren’t always shaped like round tubes. A wing can be considered a torque tube if it has a closed structure, where the skin makes a closed curve. A round tube between the pilot’s and the copilot’s rudder pedals is an easy example of a torque tube. The wings on the popular RV airplanes are also torque tubes, and for that matter, so are the ailerons, flaps, and tail cones. In airplanes we generally prefer to use some sort of thin tube for the torque tube shell because it is lighter for the same load or stiffness than other structures—if we can keep it from buckling.
So let’s start with a tube.
Figure 1 shows a simple tube with a short aileron at the end. I didn’t draw a control horn or bearings because they aren’t necessary for us at this time. Obviously any torque applied to the bottom right end of the tube will be reacted by air loads on the aileron.
Figure 1: An itty-bitty aileron attached to a robust torque tube.
For a tube, the basic equations we use are
θ = ( T * L ) / ( G * J ) ; Equation 1
and
τ = ( T * R ) / J ; Equation 2
Figure 2: A tube and its inner and outer radius.
where
θ = Twist deflection of the tube, radians
T = Applied torsion moment, inch-pounds
L = Length of section of tube that carries the torque, inches
G = Shear modulus, psi
J = Polar moment of inertia, in4 (Defined in Equation 5 below.)
τ = Shear stress, psi
R = Outer radius, inches
r = Inner radius, inches
There’s a lot to discuss here.
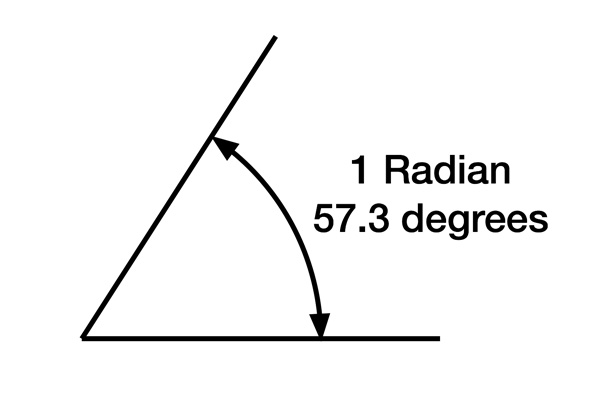
Radians are a unit of angle where the arc along the circumference for this angle is equal to the length of the radius. That’s a bit complicated, so just remember that π radians is equal to 180 degrees. Or heck, let’s make it even simpler:
Degrees twist = radians * 57.296 ; Equation 3
And you can almost always shorten that to 57.3.
Figure 3: One radian is an angle measurement equal to an angle of 57. 3 degrees.
In structural engineering, the equations for displacement angles usually give angular deflections in radians, so it’s worth remembering what it is.
The shear modulus is another useful material property. It’s related to Poisson’s ratio and the modulus of elasticity, so if you can’t find the shear modulus and you have the others, you can calculate it. It’s often supplied in materials references.
G = E / ( 2 * ( 1 + ν ) ) ; Equation 4
where
E = Modulus of elasticity, psi
ν = Poisson’s ratio, no units
The polar moment or inertia of a round tube is much like the area moment of inertia except that it’s about the radial center, rather than a neutral axis. The equations are slightly different. The polar moment of inertia for our round tube is:
J = ( π * ( R4 – r4 ) ) / 2 ; Equation 5
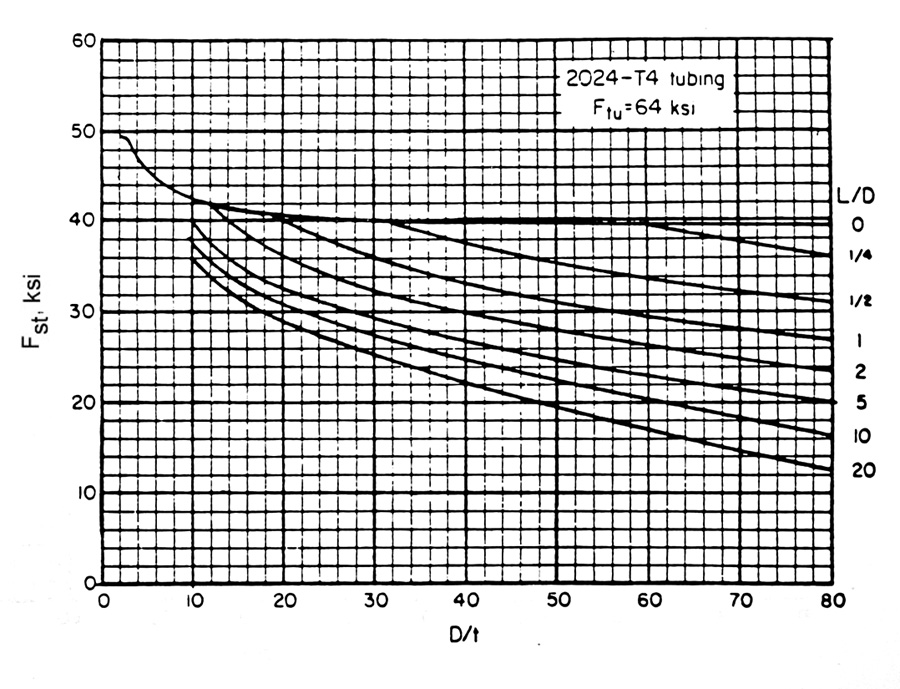
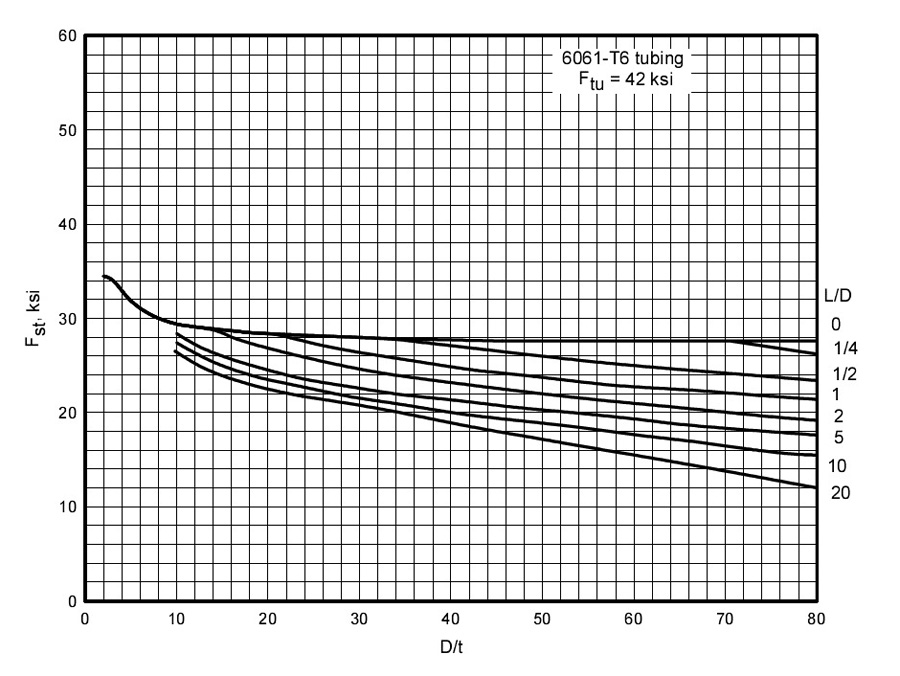
The shear stress is the stress in the tube wall. The stress is a maximum at the outer surface, but for thin walls we figure it’s constant through the thickness. Table 1 shows the ultimate shear stress, “Fsu,” for these materials, but round tubes can buckle in shear.
Table 1. Shear Modulus
Figures 4, 5, and 6 show the maximum buckling load for these materials. Note that they are affected by the diameter, the thickness, and the length:
D = Outside diameter, inches
t = Wall thickness, inches
L = Overall length of loaded tube, inches
This is an important lesson: We need to consider buckling or crippling on everything.
Figure 4: Ultimate strength of 4130 normalized tube in torsion.
Figure 5: Ultimate strength of 2024-T3 tube in torsion.
Figure 6: Ultimate strength of 6061-T6 tube in torsion.
Back at the beginning of this article, I called things like wings, fuselages and ailerons “tubes.” But they’re clearly not round tubes. What are they? They’re closed sections that have continuous structure all around their periphery. For the simpler ones that are just one odd-shaped tube, the shear stress is
τ = T / ( 2 * A * t ); Equation 6
where
τ = Shear stress in the wall, psi, maximum where the thickness is a minimum
T = Torsional moment, inch- pounds force
A = Area enclosed by the median line of the wall thickness, inch2
t = Wall thickness, inches
It’s handy to find the shear flow, too. The shear flow is the shear force per inch along the periphery, and if there’s a rib or something that transfers the load, the shear flow determines the rivet spacing.
q = T / ( 2 * A ) ; Equation 7
where
q is the shear flow, pounds force per inch
If the wall is a constant thickness, then the torsional deflection is easy to estimate:
θ = ( T * L * U ) / ( 4 * A2 * G * t )
where
θ = Twist, radians
T = Torsional moment, inch- pounds force
U = Length of the circumference of the midplane of the perimeter, inches
Usually, metal wing and fuselage structures that carry torsion and act like tubes have panels. The panels, sections of thin sheet, are checked for buckling just as if they were in compression, only now they’re in shear, and we need to use the graphs and equations that apply to panels in shear.
Sometimes we’ve got what we call “multi-cell” structures, with more than one closed section. An aluminum wing with a spar web is a common instance of this, with the leading edge forming one cell and the main part of the wing, between the spar web and the rear spar, forming the second. My RV-3B wing is built like that.
In the RV-3B right wing photo above, the leading edge is a torsion-carrying structure and so is the as-yet-uncovered main structure of the wing. The spar web is the common part between these. Multi-cell structures are a little beyond what we’re going to cover in this article, but you can read about them in E.F. Bruhn’s book, Analysis and Design of Flight Vehicle Structures, the Bell structural design manual, or the wood manual, ANC-18. The latter two are available here. We’re not going to delve into them here because the algebra can get somewhat hairy, involving long simultaneous equations. Still, if you need it, I encourage you to learn about it.
