Bolted joints are pretty simple. Drill some holes, drop a bolt into them, add a washer and a nut, and torque to the spec and you’re set. Behind the scenes, though, there’s quite a lot of engineering going on, even if we ignore the engineering of the nut and bolt themselves.
In this article I’m going to stay way from the algebra, and that means that there won’t be any analysis. It would take too much space to include the entire thing. My analysis worksheet for bolted joints is seven pages of dense math. If you want to dive into that, though, the references cover most of it.
One aspect that isn’t covered is how to design the holes the bolt goes into. Things like thickness, diameter, clearances, edge distances—all that stuff isn’t part of this article.
Basics
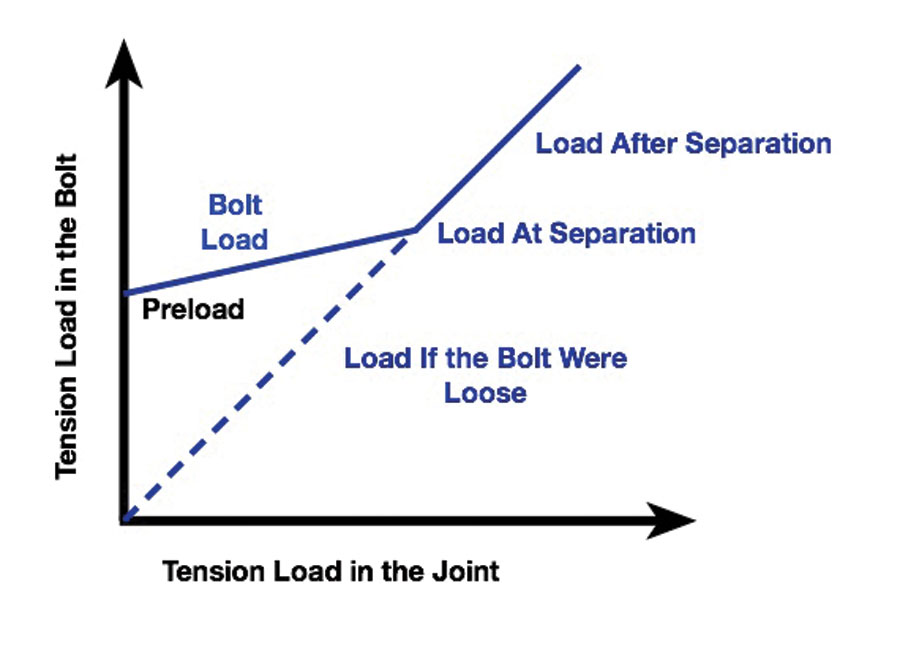
The basic concept is that tightening the bolt and nut compresses the parts that they attach, and that develops a preload. The preload puts the parts in compression and the bolt into tension. Together with the bolt, washer, and nut, the core of the joint acts as one with the bolt and shares part of any tension load that’s applied to the assembly.
With this sharing, some of the load is carried in the stack of parts of the assembly and some in the bolt. The amount of tension load that the bolt carries is proportional to the ratio of the bolt’s axial stiffness divided by the total axial stiffness of the bolt plus the compressed parts around it. This results in the bolt carrying only part of the tension load that’s applied to the whole joint, which helps the fatigue life of the nut and bolt.
The remainder of the tension load is carried through direct contact of the parts due to the compression preload. Also, the factors of safety that we use generally apply only to the load that’s in the bolt itself, rather than to the entire tension load, since it’s the bolt being analyzed. When the tension load in the bolt is greater than the bolt’s preload, the joint will separate or gap. When that happens, all of the load is carried through the bolt and nut.
Because we’d rather not have gapping occur, we try to design the joint so that it never gaps at limit load. Ideally, it wouldn’t gap even at ultimate load, but sometimes it’s not possible to achieve that.
Stiffness
Some of the better engineering texts, like Shigley’s excellent Mechanical Engineering Design, describe how to estimate the stiffness of the compressed part of the structure. Often the structure and the bolt are different materials, so it’s important to include the modulus of elasticity as you assess that. Some materials, like wood or composites, have a different modulus of elasticity in the direction parallel to the bolt’s axis than they do in the direction they are usually loaded, so you need to be careful to use the right number. For this, you’re interested in the modulus that’s in the direction of the bolt’s axis.
The stiffness calculations are based on the design of the part and are independent of the load. Like so many aspects of structural analysis, these calculations only apply when the stresses are in the linear range of the stress-strain curve.
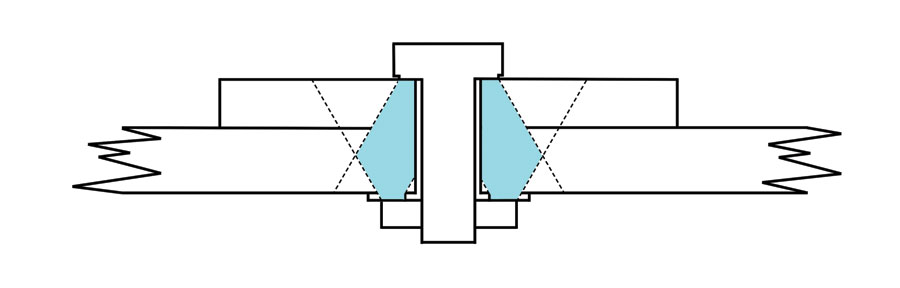
Figure 2: A bolt, washer, and nut holding together a couple of pieces of structure. The blue shaded area shows how the effective stiffness of the joint is developed from the contact areas of the bolt assembly. The compressed areas gradually expand as they go away from the mating surfaces of the bolt parts. A good mechanical engineering text will explain it.
The goal here is to find a single number—the ratio of the axial stiffness of the bolt to the axial stiffness of the whole joint. This is the ratio of load that the bolt itself will carry.
Estimating the preload generated by the torque is an iffy thing at best. You can easily find estimates that vary wildly. I use the estimates that NASA published in MSFC-STD-486, Standard, Threaded Bolts, Torque Limits For, a document issued for space shuttle payloads, which covers all of the bolts we’re ever likely to use and probably more. Whatever reference you use for predicting the preload for a given torque, pay careful attention to the description of it and its limitations. They should identify how the preload was obtained and if lubricant was used during the process. If it was, you’ll have to use lubricant too, in order to achieve the same preload to torque relationship.
The tables are for shear- and tension-loaded bolts. Typically, in the NASA document, the recommended shear torque is 60% of the torque for tension loads. Usually for kit aircraft, a designer will try to make the joint suitable for the nominal torques listed in AC 43.13-1B, Acceptable Methods, Techniques, and Practices—Aircraft Inspection and Repair. It’s good practice to do that because who knows if a mechanic in the future will know what the proper torque requirement is, if it’s different than in AC 43.13-1B. You sure can’t count on that. Still, if you do find it necessary to use a different torque in a particular instance, at least note it in your maintenance manual. You are writing a maintenance manual, aren’t you?
The nominal torque from MSFC-STD-486 generates 65% of the yield stress for the bolt’s material. Remember that we’re talking about the torque for tension-loaded bolts. Since the minimum cross-section on a bolt is at the threads, you would need to look up the bolt specification and then, after looking up the thread specification listed on it, calculate the cross-sectional area for the minor area of the threads. Then using the material specification, find 65% of the tensile yield strength—and then you have the preload. It’s a bit circuitous and takes some effort, but it’s important to do that.
The tables of torque in MSFC-STD-486 give us a nominal torque and a tolerance so that we can calculate the minimum and maximum torques. That and the work I just described gives us the minimum and maximum preloads.
Temperature
With the stiffness of the bolt and the parts of the joint having been calculated, we need to estimate the coldest and hottest temperatures in service. Then, knowing the coefficients of thermal expansion for the different materials in the joint, as well as the relative stiffnesses and the lengths of the various parts of the joint, we can find the change of preload due to the temperature. Since most joints have different materials than the bolt’s shank, temperature affects the preload. You might think that you can’t estimate the temperature range reliably, but you can probably envelope it. Think hot day, airplane sitting in the sun, dark paint, near the equator. And then switch to Alaska or Canada in the winter. Sounds improbable, doesn’t it? When I was in the U.S. Air Force, I was on a crew that tested a helicopter, painted a flat olive drab, in Florida one summer. The next winter, we tested the same helicopter in Alaska.
One of the temperature extremes will tend to add more preload and the other will tend to loosen it. The tighter one is used on every calculation having to do with strength, while the looser one is used on every calculation about separation or minimum preload. There isn’t any specific temperature factor of safety so be conservative in your estimates. Incidentally, we operated that helicopter at temperatures below -60F that winter. There were other aircraft flying, too.
At that point we’re in business.
The tension load on a bolt is all of these added together:
Maximum preload + increase of preload due to temperature + (actual tension load on the bolt * fitting factor of safety * ultimate or yield factor of safety * ratio of load that the bolt carries.)
Notice how the preload due to torque and the change in preload due to the temperature extreme add to the load on the bolt without any additional factors of safety. Those factors of safety are included in the temperature estimate that you’ll have to make, or the torque/load relationship from the NASA document.
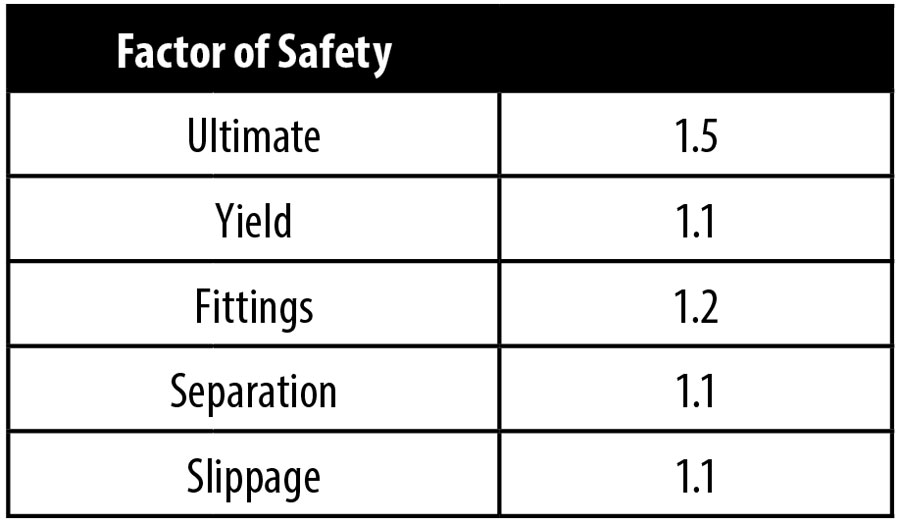
Table 1. Factors of Safety for Bolts: These are factors of safety that I’ve used in the past. Unless they are supplied by a customer or certifying agency, you can choose them for yourself. I’d recommend treating these as minimums.
Margins of Safety
The total ultimate tension load on the bolt’s threads can be compared directly to the strength of the bolt and the nut or insert, to get the ultimate margin of safety for these. The minimum tension strength is assessed at the minor area of the threads, and is often supplied in the specification for the bolts.
The yield margins of safety are calculated in the same manner.
The shank of the bolt is a different matter. If there’s any shear, then there’s also some bending, so the margin there includes the tension, the shear and the bending. The bending moment calculation is based on an estimate of the moment arm for the shank. Assuming that the threads and the head are fixed in bending (they aren’t pin-ended) and knowing where the shear plane is, we can estimate the moment arm. If there’s any clearance between the parts, you’ll have to include that in the moment arm too. The moment is based on the thicknesses of the parts, which parts carry shear, where the shear plane is, and the thickness of the gaps. Typically the moments will seem like small numbers, but the bending cross-section of most bolts is small too, and they usually generate significant stresses.
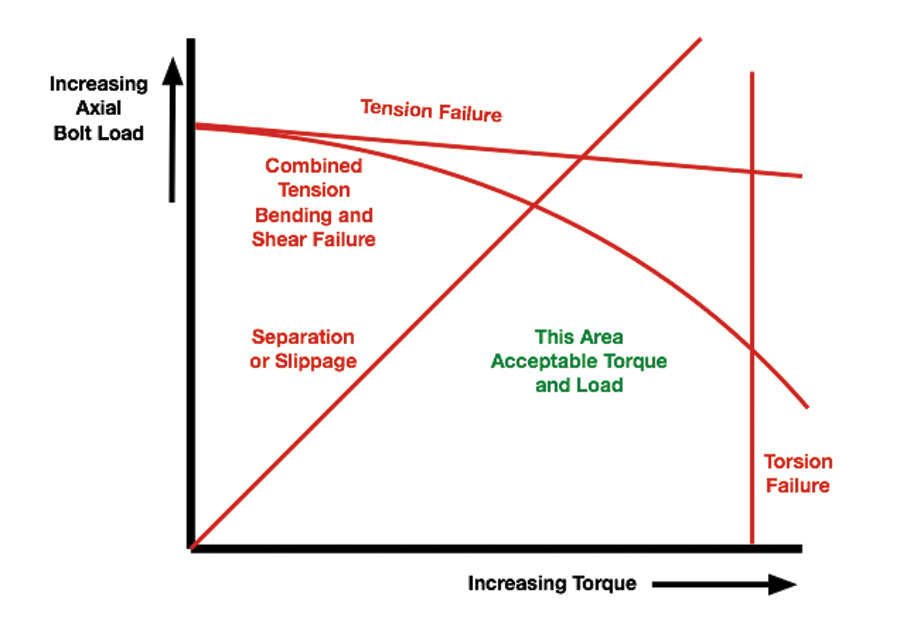
Figure 3: A successful bolt joint has enough torque that the joint doesn’t slip or separate, and not so much torque that you twist it apart during assembly. It’s got to be strong enough that it can handle the load, too. These all provide separate borders to the design space.
If there is more than one shear plane, as there would be if the bolt is in double shear, the shear force is divided among them. Either way, divided up or not, it’s carried by the cross section of the shank and the shear stress is found. This stress gets the yield or ultimate factors of safety and the fitting factor of safety, and then with the allowable shear strength, is turned into a shear stress ratio. That’s a fraction showing the shear load as the numerator and the strength as the denominator. Usually the bolt specification will include the shear strength of the shank. Be careful here, some specs give it in single shear and others give it double shear, and some don’t give it at all.
The tension load for the bolt that we previously calculated, along with the shank’s tension strength, is turned into a tension stress ratio. It needs no more factors of safety because they are already included, but you’ll need it for both the yield and the ultimate cases.
The bending stress and the factors of safety for fittings and ultimate or yield and the allowable bending strength are made into a bending stress ratio. Here it’s a good idea to look up the plastic bending strength of the bolt material because that can significantly improve this stress ratio. The Astronautic Structures Manual on the KITPLANES web site is a good place to look for that, being careful to ensure that you’re finding the appropriate material. It’s generally covered in section B 4.5. The “k” value that you’ll need for the graphs is 1.7 for round bars like bolts.
Remember that the torque for shear applications is typically 60% of the torque for tension loads? The lower preload gives a lower tension stress ratio and lets the bolt carry higher shear and bending loads. If the joint has little tension load, but considerable shear, then it might be necessary to reduce the preload below that. If so, be certain to make a note of it.
Next up is checking for separation or gapping. Don’t forget to use the temperature case that relaxes the preload and the preload that is generated from the minimum torque. Here, the load on the bolt includes the separation and fitting factors of safety, but not the yield or ultimate ones. The load on the bolt with these factors of safety must be lower than the yield strength of the bolt. Assuming that it is, then you can find the margin of safety for separation. It’s in another NASA document, NSTS 08307, Space Shuttle Criteria for Preloaded Bolts.
We’ve already verified that the bolt can carry the shear loads. Sometimes it’s worth establishing that the joint can handle the shear force through joint friction. It’s not always easy to achieve that, especially if the lower torque for shear loads is being used, because the lower preload reduces the amount of friction available. The margin of safety for this isn’t given in NSTS 08307, unfortunately, so I’m including it as a sidebar. Pay attention to my symbols since I’m not following the NSTS 08307 conventions. Here again, you’ll need to use the minimum preload after the temperature and torque tolerances are taken into consideration.
Estimating friction is at best a bit of an art. Since we don’t want the joint to slip under load, we’d need the lowest of the range of estimates for the coefficient of friction. A good argument can be made in many cases that the minimum friction available is zero friction, which is why, when a joint’s exact position is critical in shear, hole-filling fasteners like interference pins or driven rivets are used. They fill the hole, there’s no hole clearance, and thus no motion can occur without loading the bolt, and therefore no slippage. With no slippage, there’s no working of the joint and the service life is improved—exactly the same result as if we’d achieved a positive margin of safety for slippage, but with a different design approach.