In order to figure out what the loads are on an airplane, first we gather a bunch of data and then work up a V-n diagram. The “V” stand for velocity and the “n” stands for the maximum positive limit G load that the airplane can survive. Once we have that, we know how many Gs the plane can see and at what speeds, and then we can work up the loads on the wings and tail. Other loads like the ground handling loads and the engine mount loads are only partially affected by the V-n diagram, but even there, its influence is felt.
The V-n diagram is the envelope that pilots talk about when they say that they are “opening up the envelope.” The speeds it shows are the speeds that govern how the pilot operates the airplane.
Up to VA, the pilot can use full up (or nearly that much) elevator without overstressing the airplane. It takes the plane to the limit positive G load factor.
VC is the maximum speed for flying in gusty or turbulent conditions.
The never-exceed speed, VNE, is 90% of the speed VD, which is the high-speed test limit of the airplane.
Let’s draw up a sample V-n diagram and see what it gives us. The basic information that we start with are all things that the designer will establish very early in the design process. I’ve just made up some numbers here that aren’t applicable to a particular airplane.
1,400 lbs —Gross weight
123 ft2 —Wing area
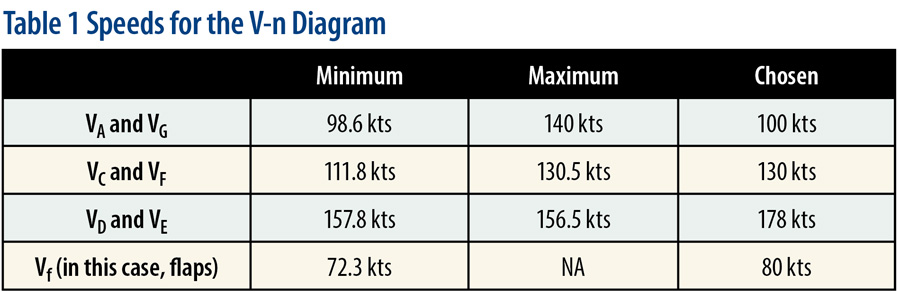
47 kts —Stalling speed, flaps up
42 kts —Stalling speed, flaps down
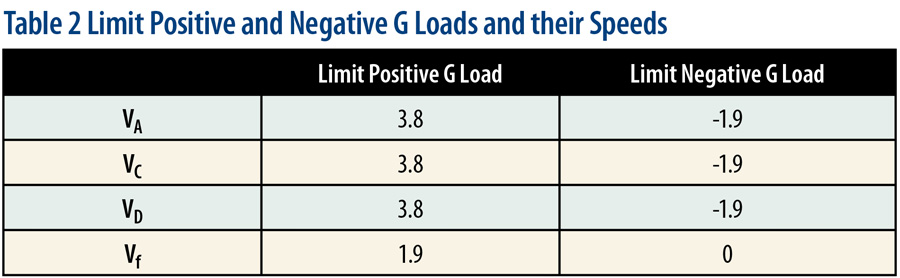
3.8 G —Limit positive load factor
145 kts —VH, top speed, sea level, level flight, maximum continuous power
For a basic reference, I’ll use FAR Part 23 Appendix A, “Simplified Design Load Criteria for Conventional Single-Engine Airplanes of 6,000 Pounds or Less Maximum Weight.” It’s easy to find online.
The title alone provides us with some cautions. We shouldn’t use it for multi-engine airplanes, shouldn’t use it for heavy iron, and if your airplane is unconventional, this probably isn’t what you should use as a guide. I’d think that “conventional” probably means that it has a tail in back, the main wings are more or less ahead of the tail, and the wings aren’t swept forward or back by more than a few degrees. It probably doesn’t have more than a single-surface flap arrangement, and the engine is probably ahead of the wing.
Now there’s nothing at all wrong with an airplane that’s not conventional in these ways; it’s just that this isn’t the best guide for calculating its loads. For airplanes that aren’t conventional in this sense, refer to the full Part 23 for a more detailed reference.
None of these regulations are required for our homebuilt Experimental aircraft. But every one of them was learned the hard way, you know, in blood. They make a good body of knowledge and experience, and are worth following.
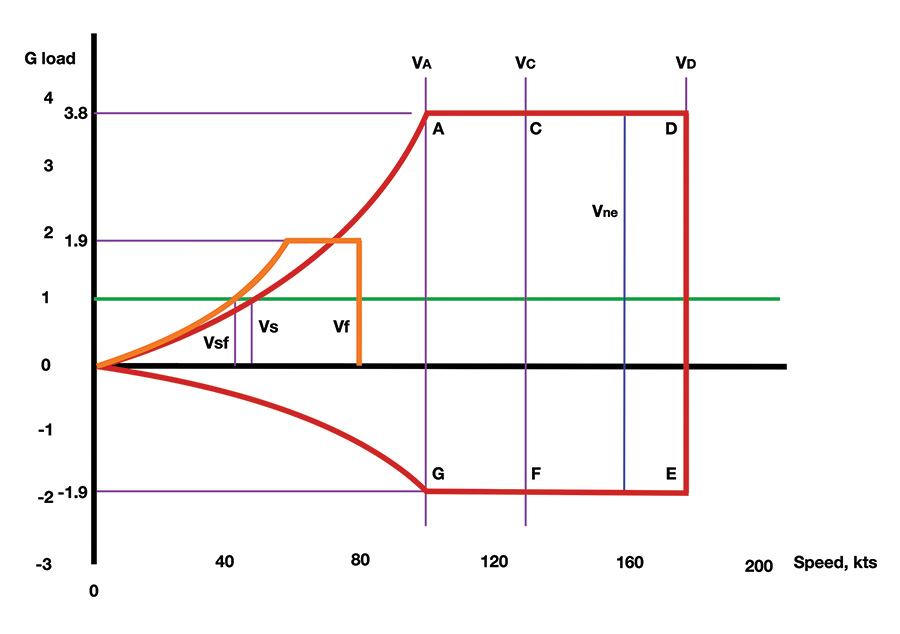
Above is the V-n diagram that we’ll work up, following the reference. We’ll calculate the speeds and G loads, starting with the basic data we’ve collected.
The first thing we need to do is calculate the parameter [n1 * W / S]1/2, which is used a lot in the V-n diagram. Grab your calculator and verify that this parameter is 6.577 for the airplane in this example. As long as you’re using the units of knots, pounds, and square feet, you can ignore the units in the equation.
From Table 1 in the reference, we know that n2 is -1/2 * n1 giving -1.9 and that n flap is 1/2 * n1 for 1.9. But before we can find the remaining G loads, we’ll need to calculate the speeds. The reference generally gives a minimum speed and then says that the speed need not exceed a maximum speed; we get to calculate both and then decide. I’ve identified those maximum speeds with the subscript “max” below, but remember that it’s not a speed limit; it’s a reminder that the speed we choose doesn’t have to be faster than this. But it could be if we have a good reason for it.
In the calculations we’ll use the number 6.577 we already came up with, rather than writing out the full equation. You can follow along in the reference if you’d like. If not, just remember that number, 6.577, is the result of working the parameter formula above, and will vary from airplane to airplane. For your airplane, figure out what the applicable number is and use that instead.
The first step is to calculate the gust penetration speed, VC. From the reference,
VCmin = 17 kts * 6.577 = 111.8 kts
VCmax ≤ .9 * VH so VCmax ≤ 130.5 kts
That funny arrow with a line underneath means “less than or equal to,” by the way, and is a math symbol.
Let’s choose 130 kts for VC:
VC = 130 kts.
Next, we find out the speeds for VD.
VDmin = 24 kts * 6.577 = 157.8 kts
VDmax ≤ 1.4 * VCmin * (n1 / 3.8)1/2 so VDmax ≤ 156.5 kts
I’d prefer that the airplane have a bit more tolerance for a pilot descending from cruise. Also, while the airplane is designed and tested to VD, that speed is later reduced to 90% of that value for the VNE that’s marked on the airspeed indicator. So let’s increase this to:
VD = 178 kts, and this will have VNE = 160 kts.
Now we should identify the maximum speed at which the pilot can use full up elevator to stall the plane, putting the maximum positive limit load on it.
VAmin = 15 kts * 6.577 = 98.6 kts
VAmax ≤ VC so VAmax ≤ 135 kts
We already know that the airplane stalls at 47 kts clean, so that speed would be 47 kts * (3.8)1/2 .
This works out to 91.6 kts. At VAmin, the airplane can pull more Gs than that. How many? 3.8 * (98.6 / 91.6)2 = 4.4 Gs, which would put it squarely in the utility category, were it a certified airplane. This airplane isn’t that strong. Still, by suggesting that the VA speed could go up from there, they felt that it was acceptable to pick higher speeds and put the burden of keeping the G load under control upon the pilot. We’ll arbitrarily select
VA = 100 kts
The final speed is the maximum speed for full flaps.
Vfmin = 11 kts * 6.577 = 72.3 kts
If we follow the same logic as we did before, we know that this minimum speed can result in a G load of 3.0 Gs, which is more than the flaps-down load factor of 1.9 that we already know about. Appendix A does not recommend a maximum speed for this condition. So let’s arbitrarily choose Vf = 80 kts and hope that the pilot will be able to get down to that speed routinely. I wanted to have it be above 75 kts since I think this relatively clean airplane could easily go that fast with flaps down. But on the other hand, I didn’t want the flap loads to dominate the wing design.
With all that, we can fill out a table for the speeds (Table 1).
With these all calculated, we can find out what the remaining G loads will be. In the reference this uses figures A1 and A2. The number at the bottom of the graphs is our good old 6.577 squared, or 56.9. There’s a short equation to work: K = VC / VCmin and for our example, K = 1.16.
Then from the figures, we learn that
n3 = n1 * +1.00 or n3 = 3.8
n4 = n1 * -.50 or n4 = -1.9
These G loads are associated with certain gust strengths. You can read the equivalent section in the full Part 23 to find out more details if you’re interested.
In Table 1, we put together the speeds. In Table 2, we have the G loads.
We now know all the speeds and G loads for the V-n diagram. I used these to draw it.
The purple flaps-down lines show the maximum limit positive (and negative, although here that’s zero) G load on the airplane when its flaps are down, and that it might see this load from 42 kts to 80 kts. The positive G load is 1.9 Gs. On an airspeed indicator, the white arc would go from 42 kts up to 80 kts.
Points A and G describe the flight conditions near the stall at its positive or negative limit loads. These are at 100 kts and 3.8 Gs positive and -1.9 Gs. Since I used 100 kts for Point A, that’s a slight bit lower load than the load that would occur at the stall at that speed. The pilot will have to be careful.
Points C and F show the flight condition at the maximum gust penetration speed of 130 kts. These G limits are 3.8 and -1.9 in this case. For this airplane, the airspeed indicator’s green arc will go from 47 kts to 130 kts.
Points D and E are for the maximum design speed of the plane. The G limits are +3.8 and -1.9 Gs again, and the speed is 178 kts. This isn’t the redline speed or the never exceed speed that’s in the pilot’s handbook, though; that’s 90% of this or 160 kts. That loss of 10% of the speed gives the operator of the airplane a slight bit of margin for flutter. It’s not a lot of margin. The test pilot must clear the plane to VD of 178 kts for flutter. But flutter being the difficult beast that it is, we give the operator this much margin. It’s not his to play with, though. It’s ours, as designers and analysts, recognizing that we need to hang on to that for safety.
The redline on the airspeed indicator will be at 160 kts and the yellow arc from 130 kts to 160 kts.
Now that we have it, what do we do with it? It defines the conditions that exist when the flight loads are developed, using the standard-day sea-level atmosphere for the dynamic pressure.
The V-n diagram doesn’t define any of the actual loads, merely the flight conditions at which they occur. For example, aileron deflections aren’t described in the diagram, but one of the Part 23 regulations, 23.455 does include aileron deflection.
The actual loads on the airplane need another bit of data. When an airplane stalls at points A or G, it’s close to the stalling angle of attack. But it’s at a lower angle of attack, not stalled, when it hits gusts at points C or F. And it’s at a still lower angle of attack at its maximum speed at points D and E. We won’t know how the loads affect the airplane until we know those angles. We might at first think that we know the airfoil lift curve so we know all that, but that’s only part of the picture.
You’ll need to adjust the basic airfoil lift curve for Reynold’s Number first, and then find the lift curve for the full three-dimensional wing. This depends on the aspect ratio, the wing sweep, and even the Mach number, small as it might be. Once you develop the lift curve for the real wing for each of the major speeds in the diagram, you’ll have a basis for figuring out the actual loads. If you can find data for the negative part of the curve, that’ll assist in calculating those parts of the envelope, too.
In engineering, we approach safety by assessing all the design conditions. So far we’ve talked about all the points on the V-n diagram. Or have we? There are three additional points worth checking just to be sure.
The lowest of these is the flap G load of 1.9 Gs combined with the stalling speed at that G load (hint: it’s (1.9)1/2 Gs * 42 kts = 58 kts). The angle of attack at this point might make it critical.
The second lowest of these is at 80 kts and flaps down and zero Gs. Since this point has the wing pushing down and the flap lift pushing up, and all the wing torsion load from the flaps, it might be critical for some parts.
The high-speed case that’s similar is at 178 kts and zero Gs. Here, there’s no flap load, but the wing has its full torsion load without lift. It’s not likely that it is a critical case, but we won’t know without checking it. So we check it—that’s what engineering is all about.
It’s important to remember that the V-n diagram doesn’t include ground loads, engine torque loads, crash loads, or other conditions. But it does describe the flight loads and is the foundation for developing them.