The materials we build our aircraft with stretch if they’re loaded with a tension force and compress if loaded with a compression force. This fundamental characteristic is important to understand in order to assess how the structure will behave while loaded.
Pull-testing machines like this one are used to generate the stress-strain curve for different materials. They pull at a low rate of strain, logging the force required at every strain increment. They can be used for compression or shear tests, too.
Axial stress is the force divided by the area of the structure, with units of pounds per square inch, or psi. The stress is determined for a specific point on the structural member, where the area is measured. The sign convention is that tension is always positive and compression always negative, except in the margin of safety equation.
The stretching or compression is called strain, and it’s the actual deflection divided by the length. Since both of these have the same unit or length, strain has units of inch/inch, or no units.
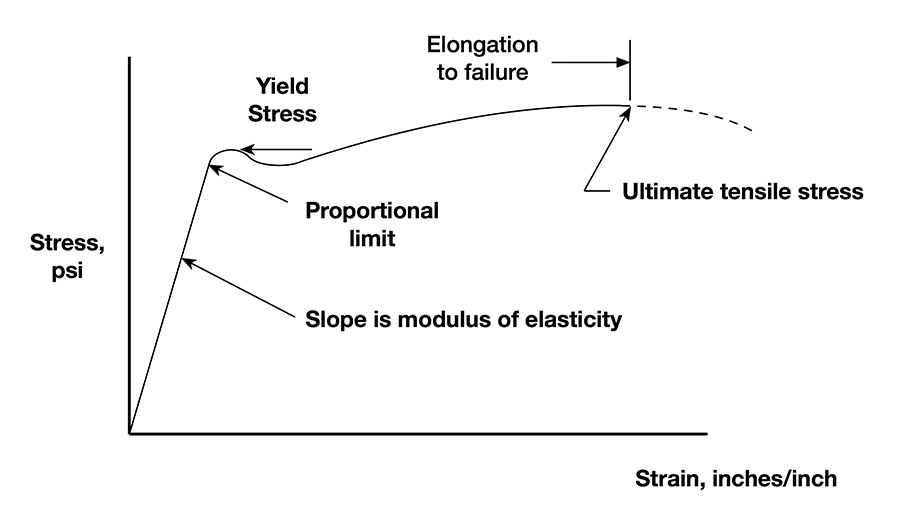
We can find a stress-strain diagram for most metals that shows the relationship between the stress and the strain for various stresses or strains. The curve shows the allowable stresses that the designer can use, unless some other issue like buckling gives lower allowable stresses, which it surely might and often does.
Please see Figure 1 for the stress strain curve of a generic aluminum alloy. It also applies to some steels and some magnesium alloys.
The modulus of elasticity “E” is a material property used to describe how stretchy or stiff a material is. Rubber has a very low modulus, while aluminum has a moderately high modulus. In the figure, the modulus of elasticity is the slope of the stress-strain curve, or the stress divided by the strain, in its linear region. There are a number of different nuances and kinds of moduli of elasticity, such as the tangent modulus or the secant modulus. For most purposes, we don’t need to get into them. They are sometimes used for things like buckling, which we’ll talk about in another article.
A very good reference for the strength of metals is MMPDS, “Metallic Materials Properties Development and Standardization.” For wood, it’s ANC-18, “Design of Wood Aircraft Structures.” Both are available here. In either, study the definitions and descriptions to learn the nuances of how the data is presented and what it means. For any other material, you’re on your own.
The yield stress is the stress that leaves a permanent strain of 0.002 inches per inch remaining when the stress is removed. It’s higher than the proportional limit, which is the maximum stress that the stress and strain follow a straight-line relationship. The proportional limit is a permanent strain remaining of only 0.0001, although some aluminum alloys have small but measurable permanent strains at stresses considerably below the proportional limit. Above this, the line starts bending ever so slightly as small, but measurable, permanent yield occurs when loaded. As the metals reference MMPDS puts it, “the industry adopted 0.002 inch/inch plastic strain is an arbitrary limit that is considered acceptable by all regulatory agencies.” The strain which occurs when a part has sustained a stress above the yield stress, after the load has been removed, is called plastic strain. It will be relatively large and permanent.
The proportional stress is not given in sources like MMPDS. If it’s important to your design, you’ll need to dig for it.
The yield stress is one of the common allowable stresses that are used during the structural analysis of an aircraft.
The ultimate stress is the tensile stress at which failure occurs and is the most common allowable stress that we usually consider.
Figure 2 shows the behavior of some steels. These have a definite yield point.
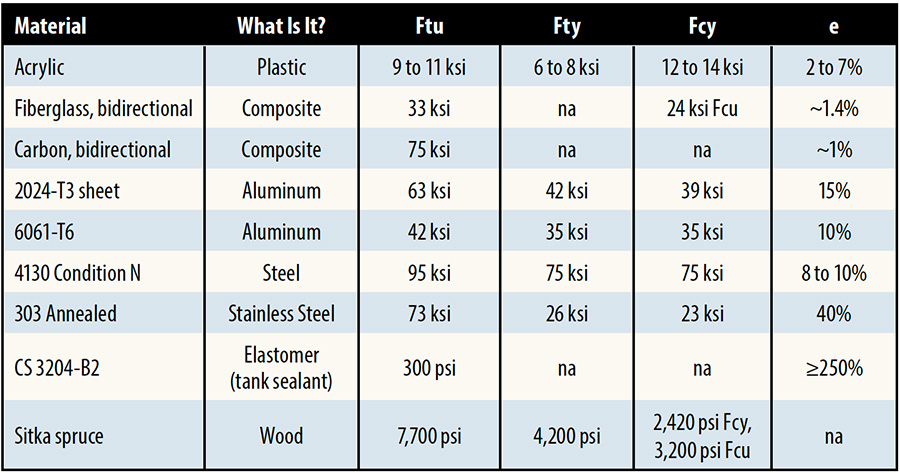
You’ll need these definitions for Table 1: First, ksi means 1,000 psi. This is a very common unit in aerospace structural engineering. Next, psi means pounds force per square inch, and this is the standard unit of stress. Be careful that you don’t mix up ksi and psi or you’ll make a tremendous mistake. And Murphy’s Law says that it’ll bite you.
Allowable stresses are usually described using the capital letter “F,” followed by the type of stress, followed by whether it’s an ultimate condition (u) or a yield condition (y). So Fcy is the symbol for the allowable compressive yield stress of a material. When actually doing the analysis, we frequently use the lower-case letter “f” to identify the predicted stress. Sometimes we use “σ,” the Greek letter sigma, for the same purpose. It’s easier to follow an analysis if you use these conventions. Be a little careful, though, as some references ignore this.
The elongation to failure is how far the material stretches (elongates) under a tension load, before tearing apart into two pieces. It’s written as “e,” and its units are provided in percent.
For all the materials in the table except the plastic and the elastomer, the properties vary slightly depending upon direction, due to the material’s manufacturing process. For the metals, I chose the smallest property value from any direction. While this at first appears like a blatant bit of conservatism, it’s not; the designer often doesn’t know which direction in the raw sheet the part will be cut from, and needs to ensure that regardless of orientation, the part will be acceptable. If it’s very important, the designer has to specify grain direction. In those cases, the part direction is specified, and the values appropriate to that direction can be used.
Composites can have a wide range of properties depending upon which fiber and matrix you’re using, how it’s woven, how it’s laid up, the angle the fibers make relative to the load, the fiber and matrix proportions, and probably a few other parameters, too. Not knowing any of that, I hunted around and found what I hope are representative properties for the amateur builder, for Table 1. Even at that, these are about 10% higher than a noted marine composite designer uses. Another thing about composites is that if you’re designing an axially-loaded structural part, it’s unlikely that you’ll be using bidirectional composites. At the very least, part of the lay-up will probably be unidirectional, and I haven’t provided strengths for that.
For the wood, I chose the lengthwise properties and 20% moisture. That much moisture might be higher than usually seen in most parts of the U.S., but the designer can’t choose where the plane will be operated, and as the moisture goes up, the strength goes down.
As you can see, there’s a very rough relationship between elongation to failure, “e,” and the difference between tensile yield stress and ultimate or failing stress. As the spread between the stresses gets greater, so does the elongation. When you’re choosing a material, keep both stresses in mind because a very low yield allowable stress might end up designing the part, where a different alloy or heat treatment might let you make the part lighter. This is certainly the case with the 300 series stainless steels in the annealed condition, where even 1/4 hard will give you significantly stronger properties. But if you’re using it for a firewall or something like that, perhaps the thickness is based on the fire resistance, and the stresses might not be an issue; then annealed is fine, and might be easier to work with, too.
The compressive strength allowables are for geometry where buckling isn’t a consideration. This would necessarily be limited to short lengths that don’t include relatively thin sections. Solid cross-sections like round bars, squares and modest rectangles, that sort of thing, would be the sort of shapes where you can use that allowable strength directly, if they are relatively short. Incidentally, if Fcu isn’t shown in your material reference, generally you can assume that Ftu is equivalent, at least for metals.
Calculating axial stress is probably the easiest thing in structural engineering. The stress is the force divided by the cross-sectional area of a part. The cross-section must be perpendicular to the applied force, and if the cross-section changes locally, use the minimum area.
f = P / A
Where
f = Limit axial stress, psi
P = Limit load, pounds force, positive in tension, negative for compression
A = Cross-sectional area, inches squared
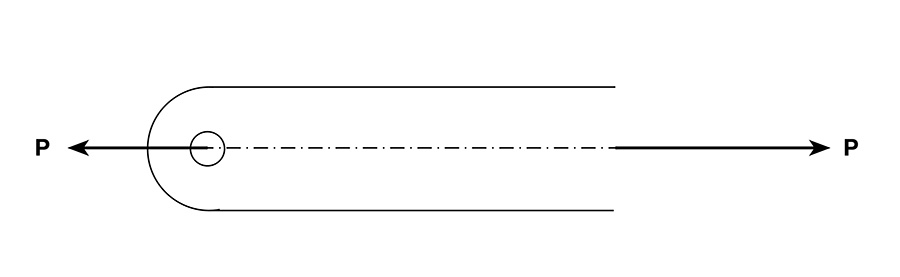
There are a few places that you can’t apply this simple axial stress. The most important is close to a hole that contains a fastener that has a load on it. See Figure 3, which shows a continuous axial member that has a single fastener through a hole in its end. Parts like this are called lugs. In the area within three hole radiuses of the center of the hole, the simple axial stress is not applicable.
Other places are where the load is clearly not perpendicular to the cross section of the part, or clearly not coaxial with a major axis of the part. If there are fasteners, the axial stress might be part of the overall stress, but the effect of the fasteners will certainly have to be considered.
Still, even with the various issues, P/A is a very important concept to understand, and fundamental to structural engineering. Except in a few places where tubes are in bending or torsion, most welded steel tube structures have their tubes axially loaded, and the axial stress governs their behavior. Tubes and other members with thin sections must be considered for buckling if there’s any compression load at all.