Most major structures on an aircraft need to support some bending. In this article, we’ll look at how a beam resists bending and how to find the bending stress. There are a variety of convenient tables in the Astronautics Structures Manual to help you actually calculate the bending moment using the loads that are applied to the beam. Look in asm-B400. Here, we’ll discuss what to do with the bending moment once you have it.
The very pretty spars for the author’s RV-3B are important enough that Van’s Aircraft sent them pre-assembled.
You can find the beam stress by using this equation:
σ = M • c / I
Where
σ is the bending stress in psi,
M is the bending moment, inch pounds force,
c is the distance from the neutral axis to the place where the stress is, inches
I is the area moment of inertia about the neutral axis, inches
This is the fundamental equation for bending. The equation tells us a few important things. If the bending moment goes up, the stress does too, proportionally. If the stress is too high, you would increase the moment of inertia to make it go down. And the equation also tells us the stress is directly proportional to the distance from the neutral axis.
Figure 1: Bending stress distribution across a beam.
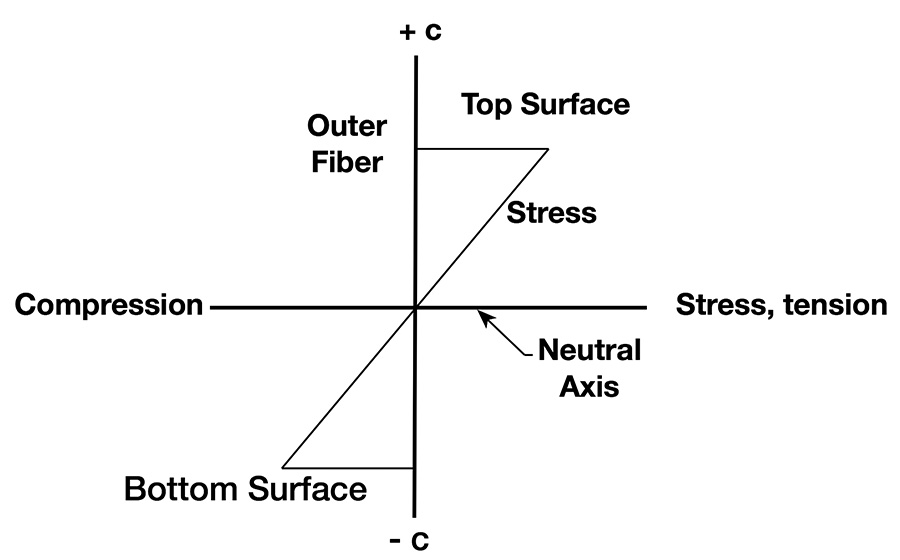
Figure 1 shows how the bending stress distributes itself across a symmetric beam. The stress is zero at the neutral axis and increases linearly as the distance from it increases. This means that at the outermost edge of the beam, farthest from the neutral axis, which we call the “outer fiber,” the stress is at maximum. But there’s still stress between the top and bottom outer fibers, and those places need to be able to carry that stress.
If there’s an axial force in the beam as, for example, there will be inboard of the struts for a strut-braced airplane, then it needs to be included. In that case, the stress is:
σ = P / A + (M • c / I)
Where
P is the axial force, pounds,
A is the cross-sectional area, square inches.
An axial stress can significantly change the stresses in a beam.
We’ll need to find the margin of safety at the tension outer fiber and the compression outer fiber, for the highest positive moment and the highest negative moment. When we do that, and show that the margin is positive, we’ve shown that the beam is at least safe in bending, which is all we’re discussing in this article. The beam might also have shear and axial compression, both of which affect stability, so then you need to analyze the beam for those loads, too, but that’s beyond this article.
Where should we check the beam? Anywhere the cross-section changes, anywhere there’s an abrupt change of load, and anywhere the load is a maximum. As an example, consider a strut-braced wingspar. For a positive flight condition, the maximum positive moment will be at the intersection of the strut. Immediately outboard of that point there’s generally zero axial force. The spar needs to be checked there. Somewhere in between the strut and the fuselage, the maximum negative moment might exist. It will have axial force in addition to the bending, and that adds to the load. If there’s a point load, from a control system or flap mount or something, check it there too. And wherever there’s a fitting or a hole, the spar will need to be checked. If the spar changes cross section, we’ll want to assess those locations as well.
Figure 2: An example cross-section of an extruded beam.
When you’re figuring out the spar section to use for analysis, be sure to include any holes that are nearby the section. Holes count as gaps, with one exception: hole-filling fasteners like driven rivets can be used if carrying compression—but only compression—and even then only the shank can be used, not a countersunk head or a dimple. Dimples and countersinks act like holes.
See Figure 2, which shows a cross-section of an aluminum extrusion. This extrusion uses three of the fundamental shapes that are often used to assess beams. The sidebar on section properties shows how to calculate the properties of the more common basic cross sectional shapes. If you need a shape that’s not in the sidebar, you can look it up online.
Table 1: Geometry of the Example Beam’s Individual Elements
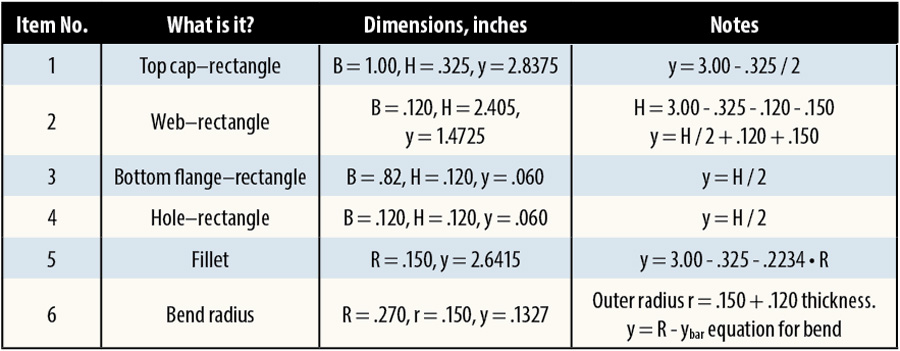
Now we’ll calculate the section properties of this beam. We’ll find the area, the moment of inertia, and the location of the neutral axis. We start with Table 1, which shows the salient facts of the individual elements in the spar.
Using the information in Table 1 and the sidebar on section properties, we next calculate some data for the spar, putting the section properties into a table like Table 2. The columns include:
Item: An identifier. I number my elements.
A: The area of the cross-section, inches squared. If it’s a hole, it’s negative.
y: The distance from the reference to the neutral axis (the x-x axis) of this element. Positive is upward from the reference line and below it, y is negative.
A • y: Multiply the element’s area by its distance.
A • y2: Multiply the A * y calculated value by y again.
Io: Calculate the element’s own moment of inertia, about its own neutral axis.
Table 2: Example—A Cross Section of an Extruded Beam.
Remember, if a negative number multiplies a positive number, the result is a negative number. If you multiply two negative numbers together, the result is positive.
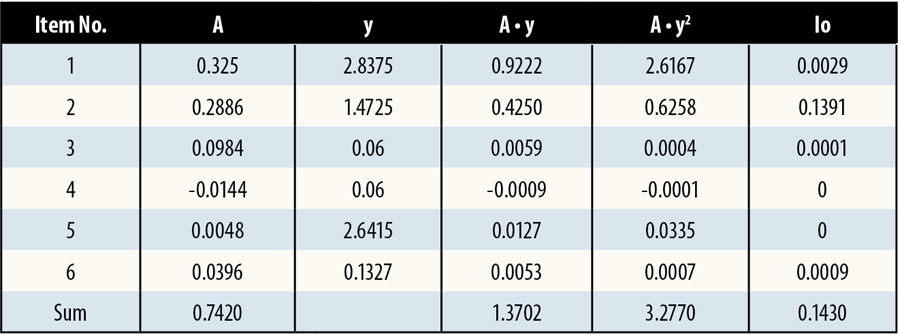
The bottom row of the table gives us the overall properties of the beam.
A: Sum the individual element areas and put the total here. Units are inches2.
A • y: Sum the individual element area • distance and put the total here. Units are inches3.
A • y2: Sum the individual element area • distance squared and put the total here. Units are inches4.
Io: Sum the individual element inertias and put the total here. Units are inches4.
Then under the table, make these calculations:
Ybar = Sum A • y / Sum A
Ybar, with units of inches, is the position of the neutral axis from the reference for your beam. Incidentally, in this article, I’m using ybar to indicate the individual element property and without the subscript Ybar to indicate the overall beam’s property.
We can find the spar’s moment of inertia, using the values summed at the bottom of the table:
I = Sum (A • y2) + Sum (Io) – Sum (Area) • ybar2
“I” is the overall moment of inertia for the beam. It’s more formally called the “area moment of inertia” to differentiate it from the mass moment of inertia. However, usually during stress analysis, we drop the word “area” because the meaning is clear from the context.
Once in a while, when considering buckling situations, we’ll also need to find the radius of gyration, ρ:
ρ = [I / A]1/2
Or another way to describe it is:
ρ2 = I / A
If you need it, use whichever form is appropriate. Physically, it’s the radius from an axis about which the area is distributed, if it were all located in a ring about the axis. That description’s not useful and I much prefer the equation.
For our example, to tie the data into the previous figures and analysis.
Area = 0.7420 inch2
Ybar = 1.3702 / 0.7420 = 1.8466 inches
I = 3.2770 + 0.1430 – 0.7420 • 1.84662 = 0.8897 inch4
Now that we’ve done the hard work, we can find out what the stresses are on the beam. We need to know what the bending moment is. For this example, that’s 17,900 inch-pounds force, and that’s the ultimate moment. These moments are positive, and by definition that means the compression stresses are on the top. We also need “c,” the distance from the neutral axis to the outer fiber.
ct = 3.00 – 1.8466 = 1.1534 inches to the top surface.
cb = 1.8466 inches to the bottom surface.
Finally, we can find the stress:
ft = 17,900 • 1.1534 / 0.8897 = -23,205 psi for the top surface. It’s negative because the top surface is in compression.
fb = 17,900 • 1.8466 / 0.8897 = 37,152 psi tension on the bottom surface.
For now, we’ll have to use the ultimate tensile stress and the yield compressive stress as the allowable strengths, and calculate the ultimate margins of safety. This isn’t a conservative calculation though, because it didn’t cover buckling. In another article we’ll discuss crippling, a type of buckling instability that will reduce the strength of many beams and other structures. Crippling or other types of buckling are prevalent all through aircraft construction and are a major design issue.
FSu = 1.5 Ultimate factor of safety.
Ftu = 63,000 psi Ultimate tensile strength of 2024-T3, 0.063 thick (or 2024-T351 plate, thick enough to be made into a cap).
Fcy = 39,000 psi Yield compression strength for these materials.
The margins of safety are:
For the top, in compression (and worth noting here that often in the margin of safety equation, the minus signs are unnecessary; I’ve included them for clarity):
For the bottom, in tension:
S = -39,000 psi / (1.5 • (-23,205 psi)) – 1 = +0.120
It’s normal good practice to include the + signs in the result to make certain that readers understand that your margins of safety are positive. We’d also note which load condition produces these margins, important since another load condition will give different margins of safety.
Another approach to finding the strength of a metal beam is to use a concept called “plastic bending.” In some cases, plastic bending will provide higher strength than using the ultimate tensile strength of the material. The increase in strength is dependent upon the shape and the material. You can read more about it in ASM section B4.5.0. If buckling is critical, though, plastic bending might not help much. The bending strengths of wood beams include the shape characteristics, if you follow ANC-18.
In some cases, the fatigue life of a beam can be important and that might also affect the allowable stress on the beam, especially if there are changes of contour or holes. These things are beyond the scope of this article as well.
