The job of the wing is to generate lift to hold the airplane up and to maneuver. For a given wing, the amount of lift it can produce varies with airspeed. To maintain flight, the wing must be able to produce a lift equal to the weight of the airplane. Any additional lift the wing can produce allows the airplane to maneuver. How much “lift margin” the airplane has at any airspeed is important and determines what the airplane can do.
In discussing lift and maneuvering, it is useful to think in terms of the load factor the airplane can pull. The load factor, or G load of the airplane, is the total lift divided by the weight of the airplane.
Load-Factor Margin
There is an airspeed at which the wing, flying at its angle of attack for maximum lift, can just produce enough lift to equal the weight of the airplane. This is the level-flight stall speed. The maximum load factor the airplane can generate is 1.0, and the load-factor margin is zero. As airspeed increases above stall speed, the ability of the wing to lift increases proportionally to the square of the airspeed, and it becomes possible for the airplane to turn or maneuver without stalling. The load-factor margin, which is the number of G the airplane can pull above the 1.0 needed to maintain flight, determines how hard the airplane can maneuver.
Figure 1 shows the maximum load factor the wing can generate for an airplane with a wing loading and maximum lift coefficient that would make it legal in the Light Sport category. Notice that the maximum load factor is 1.0 at 44 knots.
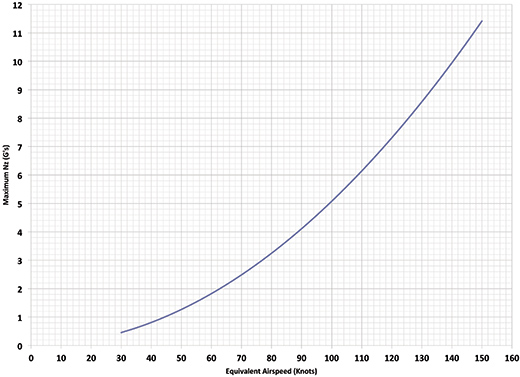
Figure 1.
As we can see from the curve, the margin above this minimum 1.0 load factor increases relatively rapidly with increasing airspeed. At about 63 knots, the airplane can pull 2 G, which means it could sustain a 60° banked turn without stalling. By the time the airspeed reaches 120 knots (the legal maximum cruise for a Light Sport airplane), the wing is capable of generating enough lift to pull 7 G.
In practical terms, this means the airplane will have a maneuvering speed well below this theoretical cruise speed, even if the structure is designed to the FAA aerobatic category maximum limit load of 6 G. It’s important to be aware of how much load the airplane can generate aerodynamically, particularly when flying clean airplanes with relatively low wing loadings. As we can see from our example, such an airplane can generate enough lift to break the structure at a relatively low speed. Our example airplane would have a maneuvering speed of 109 knots.
The Physics of Turns
Another area where the load-factor margin becomes important is in turning flight, particularly at low airspeed near the ground, such as is the case in the traffic pattern.
The velocity of an object is a vector quantity. It has both a magnitude and a direction. Acceleration is a change in velocity and can be a change in either or both the direction and the magnitude of the velocity. A turning airplane is continuously accelerating toward the center of the turn, even though its speed, which is the magnitude of the velocity, is constant. Newton tells us that a force must act on a mass to cause acceleration. In a turning airplane, this force is the lift of the wings. By banking the airplane, the pilot causes some of the lift to act horizontally. It is this component of the lift that curves the flight path in the direction of the bank.
While the horizontal component of the lift of a banking airplane is curving the flight path, the vertical component is still holding the airplane up against gravity. In a level turn, the vertical-lift component must equal the weight of the airplane. The total lift required to perform the turn is the vector sum of the horizontal- and vertical-lift components. Accordingly, the total lift in any level turn is greater than the weight of the airplane. As bank angle increases, the horizontal component of lift gets larger in relation to the vertical component. The vertical-lift component is constant, so the total lift required increases with increasing bank angle. The load factor in a constant-altitude turn is given by:
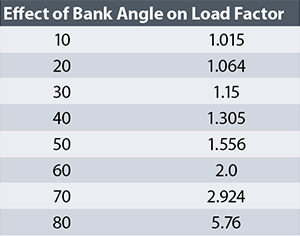
N = 1/[cosine(bank angle)]
N = Load factor in G.
The table shows the influence of bank angle on the load factor required to maintain a level turn. Note that as bank angle increases, the rate of load-factor increase with bank angle also increases. Going from zero bank to 10° only increases load factor by 0.015 G. Adding 10° of bank to go from 70° to 80° increases load factor by 2.84 G.
This phenomenon is a key ingredient in the classic stall/spin on the base-to-final-turn scenario. To increase load factor, the lift generated by the wing must increase. The pilot does this by pulling back on the stick and increasing the angle of attack of the airplane. As we have just seen, the amount of extra lift required by a given bank-angle increase is much larger if the airplane is already in a steep bank than it would be in a more gentle turn. This may catch the pilot by surprise if he is used to shallower turns. At the low airspeed typical in the pattern, the wing cannot develop enough lift to maintain the required load factor and will stall as the pilot attempts to increase lift by pulling.
Figure 2 shows the load-factor margin of our example airplane as a function of bank angle at several airspeeds.
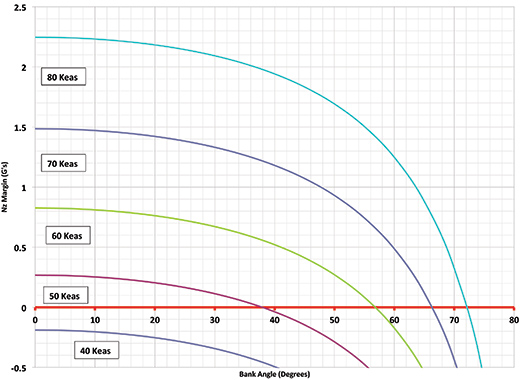
Figure 2.
Notice first how rapidly all of the curves fall off as bank angle increases. For example, if we look at the curve for 70 knots, which would be a typical traffic-pattern airspeed for this airplane, the airplane has a load-factor margin of about 1.5 G, wings level. Increasing the bank angle to 30° only reduces this margin to slightly above 1.3. This means that in a 30° banked turn at 70 knots, this airplane still has a significant amount of excess lift available to tighten the turn, or pull up. The pilot can increase the bank angle significantly from the initial 30° without stalling the airplane.
If we now increase bank angle to 60°, the picture changes dramatically. The load-factor margin falls to 0.5 G. The wing is generating most of the lift it can, and the pilot can only ask for another half G of load factor before the airplane stalls. Most importantly, the G margin goes to zero at about 66° of bank. This means that in a 60° banked turn, the airplane will stall if the pilot increases bank by only 6° and pulls to try to maintain constant airspeed.
Understanding this rapid loss of lift margin with increasing bank angle is important for safe flying in the traffic pattern. A pilot who normally makes traffic-pattern turns at moderate bank angles (around 30°) is used to being able to adjust the radius of the base to final turn, to line up with the runway by varying bank angle significantly around the initial bank used to establish the turn. If the pilot overshoots the initial turn and establishes a steeper banked turn to compensate, there is very little additional margin left. The ability to further tighten the turn with what seems to be a moderate bank-angle increase is gone; attempting to do so will stall the airplane. As the curves in Figure 2 show, this loss in margin to increase bank angle happens quickly as the basic bank angle exceeds about 45°.
FAR Part 23 designates the approach reference airspeed as not less than 1.3 times the level-flight 1-G stall speed. At this airspeed, an airplane is capable of generating a maximum load factor of 1.69, so it will have 0.69-G load-factor margin in level flight. In a 30° bank, it will have just over 0.5-G margin, and in a 45° bank, the margin will fall to 0.25 G. At the FAR 23-designated approach speed, the airplane cannot be trimmed in a 60° bank without stalling.

![]()
Barnaby Wainfan is a principal aerodynamics engineer for Northrop Grumman’s Advanced Design organization. A private pilot with single engine and glider ratings, Barnaby has been involved in the design of unconventional airplanes including canards, joined wings, flying wings and some too strange to fall into any known category.













