For most airplanes, the majority of a mission is spent in level flight at 1 G. To get to its cruise point, the airplane must climb, and to get where it needs to go, it must turn at some point during the flight. Both climbs and turns place greater energy requirements on the airplane than cruise. In climb, the airplane must gain potential energy by increasing altitude, and this energy must come from the engine. In turns, the total drag is higher than it is in cruise. The energy to overcome this drag must come either from the engine, or from sacrificing potential energy by descending. The total energy available to the pilot to climb and maneuver the airplane is a critical parameter for safe flight.
Specific Excess Power
At any given flight condition, the engine can provide a certain amount of thrust, and the airplane has a certain amount of drag. The thrust from the engine can be used to overcome the drag. The excess thrust is the amount of thrust available above that required to overcome the drag. If there is excess thrust available, it can be used to climb.
The standard way of measuring excess thrust is to put it in terms of the rate of climb that could be generated at that flight condition at full throttle. This is called Specific Excess Power (PS) and is expressed in feet per minute (fpm) of potential climb. If an airplane has positive PS, it can climb at the airspeed and load factor at which it is flying. If PS is zero, the airplane can maintain its altitude, airspeed and load factor, but it cannot climb. If PS is negative, the airplane cannot maintain its altitude, airspeed and load factor at full throttle. It must either descend or unload to maintain airspeed.
It is important for a pilot to have a sense of the energy state of the airplane and be aware of how much PS is available at any point in the flight.
Understanding the Physics of Turns
The velocity of an object is a vector quantity; it has both a magnitude and a direction. An acceleration is a change in velocity, and can be a change in either the direction and/or the magnitude of the velocity. A turning airplane is continuously accelerating toward the center of the turn even though its speed, which is the magnitude of the velocity, is constant. A force must act on a mass to cause acceleration. In the case of a turning airplane, this force is the lift of the wings. By banking the airplane, the pilot aims some of the lift horizontally in the direction of the desired turn. It is this component of the lift that curves the flight path in the direction of the bank.
While the horizontal component of the lift is curving the flight path, the vertical component is still holding the airplane up against gravity. In a level turn, the vertical lift component must equal the weight of the airplane. The total lift required to perform the turn is the vector sum of the horizontal and vertical lift components. The total lift in any level turn is greater than the weight of the airplane. As bank angle increases, the horizontal component of lift gets larger in relation to the vertical component. The vertical lift component is constant, so the total lift required increases with increasing bank angle.
The load factor, or G load, of the airplane is the total lift divided by the weight of the airplane. It is in units of gravities or G. In a constant-altitude turn, the load factor is given by:
N = 1 / (cosine (bank angle))
N = load factor in G.
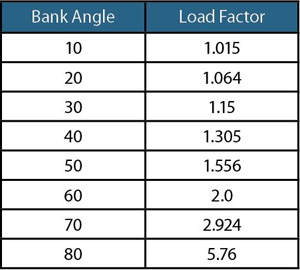
Table 1: The effect of bank angle on load factor. As bank angle increases, the load factor rate also increases.
Table 1 shows the influence of bank angle on the load factor required to maintain a level turn. Note that as bank angle increases, the rate of load factor increase with bank angle also increases. Going from zero bank to 10 increases load factor by only 0.015 G. Adding 10 of bank to go from 70 to 80 increases load factor by 2.84 G.
This is critically important, not only from the viewpoint of avoiding an accelerated stall, but also from an energy perspective. As the load factor increases, the total lift increases. This increases the induced drag, and because induced drag increases with lift squared, the effect on PS can be dramatic.
Effect of Maneuvering onSpecific Excess Power
The following example illustrates the effect that the drag increase due to maneuvering can have on aircraft performance. Our example airplane is representative of a Light Sport trainer. It has a wingspan of 30 feet, weighs 1320 pounds and has a 100-horsepower engine.
Figure 1 shows curves of full-throttle PS for this airplane at several load factors. Looking first at the 1 G curve, we note that the airplane has a top speed of 113 knots (zero PS) and a maximum climb rate of about 770 fpm at 73 knots.
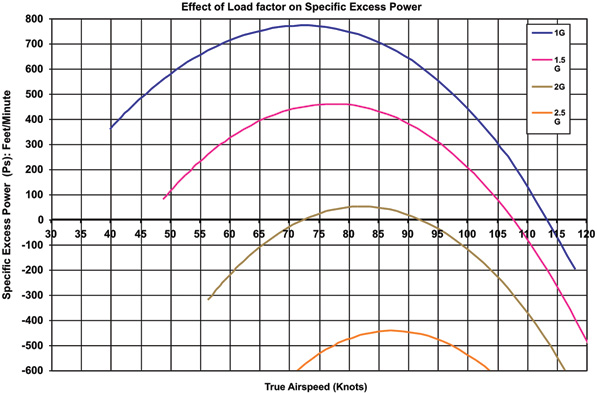
Figure 1.
Looking now at the 1.5 G curve, we see that performance has dropped significantly. Maximum PS is only about 460 fpm, and zero PS now comes at 107 knots. Note also that the airspeed for maximum PS has increased from the 1 G case. This last item is important because the maneuver will typically be initiated from level flight, so the airspeed may have to change to get maximum performance from the airplane.
At a load factor of 2, the airplane is nearing its performance limits. It has positive PS only from 73 to 93 knots, and the maximum PS has dropped to about 50 fpm. At load factors greater than 2, the airplane cannot simultaneously maintain airspeed and altitude, and it must descend to avoid decelerating.
To see how this change in performance with load factor can affect safety in a normal flying situation, we now turn our attention to Figure 2, which shows the effect of initiating a turn when our example airplane is flying at the airspeed for best rate of climb after takeoff.
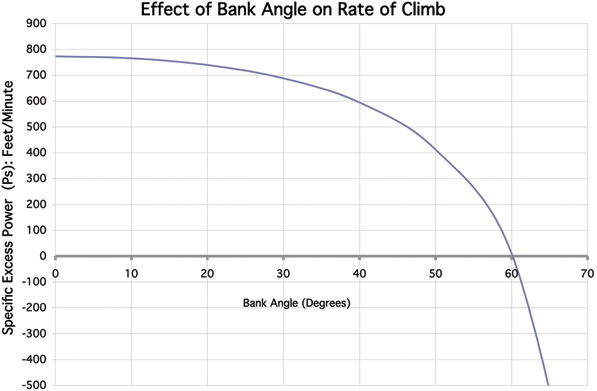
Figure 2.
As long as the pilot keeps the turn gentle, the effect of the turn on the airplanes climb rate is relatively small. In a 30 banked turn, the maximum rate of climb degrades about 10%, from 770 fpm to about 690 fpm. The pilot can hold airspeed and attitude, and nothing dramatic will happen.
As the bank angle exceeds 30, the ability of the airplane to keep climbing degrades rapidly. At 45 bank, the climb rate has decreased by more than 200 fpm. If the pilot does not lower the nose significantly, the airspeed will start to drop.
Beyond 45 bank, the airplanes performance decreases rapidly. By the time a 60 bank is reached, the airplane can no longer climb. If the pilot were to attempt a steep turn shortly after takeoff, the airplane would stop climbing during the turn. If the pilot continued trying to hold attitude during the turn to force the airplane to climb, the airspeed would decrease rapidly, and a departure stall would ensue.
Particularly in low-powered aircraft, increasing the load factor erodes the airplanes ability to climb and maintain airspeed relatively quickly. Pilots should learn the capabilities of their airplanes, and always be aware of the amount of energy they have available to maintain flight.

![]()
Barnaby Wainfan is a principal aerodynamics engineer for Northrop Grummans Advanced Design organization. A private pilot with single engine and glider ratings, Barnaby has been involved in the design of unconventional airplanes including canards, joined wings, flying wings and some too strange to fall into any known category.













