Most of our aircraft have some parts that carry mostly axial forces. These are often things like wingstruts, pushrods, and nearly all of the pieces of welded steel tube trusses. When they carry compressive loads, their designer needs to figure out how to make them carry that load without buckling. Since aircraft must be designed for both positive and negative flight loads, there’s probably at least one load case that puts almost any part on the plane into compression. Usually that load condition is the critical one for the part, and being critical, that particular load governs that aspect of the design.
Imagine a long, skinny tube in compression. It might be a wingstrut without jury struts, like the ones on the Kolb Mark III Xtra shown in Figure 1. Our generic strut has some sort of single-fastener connection at each end, so that the strut is free to rotate about the fastener. While the fastener acts like a hinge in one direction, in the other direction it’s not especially stiff and, in fact, it practically acts like a hinge in that direction too. These ends can rotate in any direction except perhaps in torsion. A strut or column with this type of end is a “pin-ended column,” and if the compression load is too high, it’ll buckle. Instability is another term for buckling. Buckling and instability are interchangeable terms, so if you’re looking up one and you can’t find what you’re looking for, try the other. Either way, when it comes to struts, we don’t want it to happen.
The load that these columns carry depends on a lot of things. Let’s assume that the column or strut:
- Has a constant cross section except at the end fittings. That is, it’s not tapered.
- It’s all the same material, except at the short end fittings.
- Its cross section has at least one axis of symmetry.
- The cross section is closed, like a tube. In fact, tubes are what we’ll be discussing here.
- It’s straight.
- Any side loads are tiny.
- The load is concentric or coaxial with the long axis—that is, the ends aren’t eccentric.
It’s still possible to find out the strength of a strut or column that fails one or more of these assumptions, but we can’t do it in this article.
Before we can get very far with this, we need to introduce some new terms: the end fixity and radius of gyration.
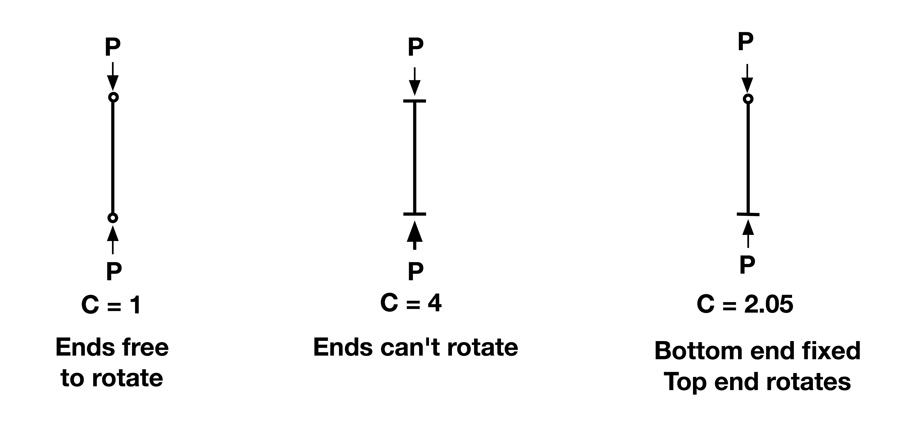
The end fixity describes how rigid the ends are. There are really only three possible cases that don’t require considerable analysis complexity: free, pin-ended, and fixed. In aircraft, a column with a free end has negligible structural utility, so we won’t discuss it. We’ve already talked about a pin-ended condition, where the column is able to rotate but not move laterally. If it has a fixed end, that end prevents rotation as well as lateral movement.
Figure 2 shows a few of the more common end fixities and the numeric value of C (sometimes the lower-case c is used), the symbol for fixity in column analysis. There’s an important gotcha buried in these, though, and that’s the question of how rigid is the actual fixed end? Will it maintain its rigidity as the load increases? Is it part of a larger structure, such as a welded truss, in which all the elements might be loaded, and in which the whole joint is rotating because of that? That’s a particularly sneaky way for what looks like a fixed end to actually be a pin end. In structural analysis, we have to be certain that we don’t error on the side of weakness or possible failure. Therefore, if we haven’t made certain that the fixed ends are actually rigid, we should assume that they are pinned.
The next concept is the radius of gyration. It’s the radius about which, were the whole area concentrated there, the element would behave the same as it actually does. However, I’ve never found that definition to be as helpful as the mathematical definition of it:
Equation 1: ρ = (I/A)
Where
ρ is the radius of gyration, inches
I is the area moment of inertia, inches4
A is the cross sectional area, inches2
Although what we’re discussing today isn’t limited to round tubes, often that’s what we use. For a round tube,
R = D/2 Outside radius, inches
r = R – t Inside radius, inches
Equation 2: = (R4 – r4) * π/ 4
Area moment of inertia, inches4 And
A= (R2 – r2) * π
Equation 3: Area, inches2
Where
D is the outside diameter, inches
t is the wall thickness, inches
This gives you enough to solve for ρ. For streamline sections, download the file Streamline-Tube-Data.xls.
We’ll also need:
Equation 4: D/t
It’s just called “D over t,” nothing fancy here.
Another term:
L’ = L / √C
Where
L is the length of the strut, pin center to pin center, inches
C is the fixity from Figure 2, no units
With all these, calculate L’/ρ. This is a number we’ll use a lot. We pronounce L’ “L prime,” by the way.
Look at Figure 3. You’ll see that it has two graphs. The inset graph shows the upper limit for the allowable crushing stress as a function of the D/t ratio. You can see that as the tube gets thinner (that is, the D/t number gets bigger), the allowable crushing stress goes down. Crushing stress is a bit of a misnomer; what’s occurring is local buckling of the tube’s wall. The overall column buckling of the tube is different from the local crippling, which is why these charts include both the effect of length and the effect of the wall thickness. For a particular part, one or the other might dominate and control the design, so you’ll need to check both and use the lower value.
Figure 3: Example of column strength data. (Don’t use this graph in an actual design—it’s just for illustration.)
Some graphs have tick marks on the main curve to show where the D/t ratio starts to dominate, but not all of them.
When tubes are welded, the weld strength can be a cutoff stress; no matter the tube’s geometry, even if it doesn’t buckle, its weld can still fail. For steels, that’s often shown on the graph. Typically for 4130 that’s normalized, the maximum stress in weld-affected places is shown as a cutoff limiting the curve.
For other shapes than round or streamline tubing, and other materials than 2024-T3 or 6061-T6 aluminum and 4130 normalized (that is, sold as condition N) round tubing, you’ll have to analyze it the hard way. Still, even there, if you have a long pin-ended column and you know its major inertia (the smaller number of the two moments of inertia), Euler’s column buckling equation will be handy (“Euler” is pronounced “Oiler,” just so you know):
Equation 5: Pe = π2 * Ec * I / L2
Where
Ec is the modulus of elasticity for compression, psi
Pe is the compression force, pounds, that will buckle the strut
L is the pin-to-pin length, inches
I is the smaller of the moments of inertia inches4
(C = 1 for pin-ended columns, so we didn’t need to put it in this equation.)
Euler’s equation is a fundamental structural analysis equation. I use this equation a lot to estimate what the moment of inertia ought to be. It might not be the final value, but it’s a place to start. Unfortunately it’s limited to large values of L’/ρ, such as over 80 or 100, so in most cases you’ll also need to check local crippling. One thing about local crippling is that it often causes some local yielding and the strut will never straighten out again. If that happens, its strength is ruined, and therefore it’s an ultimate condition.
You’ll have to get the minimum area moment of inertia for a particular cross section from the vendor or calculate it yourself.
You’ve probably noticed by now that if you can only reduce the term L’/ρ, that the strength improves considerably. One way to do that is simply to reduce the length of the column by adding jury struts. These small struts intersect the main strut in the middle and brace it to prevent buckling. They are usually effectively pin-ended, even if they’re clamped to the main strut. This is because they offer no bending rigidity to the main strut. Since the main strut has a point of inflection at the jury strut connection, the main strut’s rotation there means that the jury strut is pin-ended. If they’re in the middle of the main strut, that reduces the length of the main strut by two. That’s a big improvement since the length squared is in the denominator.
If you want the lightest-weight strut, make it of aluminum. Because its modulus of elasticity is lower than steel’s, that forces the size to be larger for the same column buckling strength. Since its density is lower than steel’s, the weight is lower. But if you want the lightest-drag strut, make it from steel. The higher modulus of elasticity pays off here in smaller size.
What happens when a strut or column buckles? That depends a lot on what’s happening with the strut. If there’s local crippling and the wall is distorting, it’ll probably carry some load, but not much more than the load at the onset of buckling. It’s limited because the cross section is changing and that will probably adversely affect its stiffness in that area; that is, it’s on the verge of collapse. If it’s yielding, even locally, then that also causes some reduced stiffness—and local crippling nearly always means that there’s some local yielding. Both of these lower the strength, and if either is present, you can’t count on any load available beyond the onset of buckling.
But if the strut is a long strut, with L’/ρ greater than 100, it doesn’t have any local crippling, and if the stresses are still wholly in the elastic range, it can carry additional load after it buckles. The cost for that will be much, much higher deflections and a lot of bending. A yardstick is a good example. Compress it lengthwise, and until it buckles it’ll have low deflections. When it does buckle, it will deflect a lot as it bends. An estimate of the post-buckling axial deflection is:
Equation 6: e = 2 * L * ΔP/Pe
Where
e is the axial deflection, inches, after buckling
L is the unbuckled initial length of the strut, inches
ΔP is the post-buckling increase in load (just the increase), pounds force
Pe is the Euler buckling load, pounds force
This suggests that if the load increases by 10% past the buckling load, the additional axial deflection will be about 20% of the original length of the strut—that’s huge. Nevertheless, this probably won’t matter. If it buckles, it’ll be bending and that, combined with the compression load, could fail the strut. And even if it doesn’t fail, it’ll be deflecting so much that other issues will arise, such as control system interference or even flutter. I recommend that you treat column buckling as an ultimate failure and not rely on any post-buckling load capability. J
References
1. Analysis & Design of Flight Vehicle Structures, E. F. Bruhn, 1973, has an excellent discussion of the whole matter, including lots of tables and graphs, that can take you well beyond round and streamline tubes. Although thorough, it can be difficult to find what you need.
The following references can be downloaded.
2. Metallic Materials and Elements for Aerospace Vehicle Structures, MIL-HDBK-5H, 1998, is an excellent source for data and includes other materials than the ones I discussed here.
3. Metallic Materials Properties Development and Standardization (MMPDS) is an FAA document that supersedes MIL-HDBK-5. Both are largely the same, especially for the metals and fasteners we’re most likely to use.
4. Strength of Metal Aircraft Elements, ANC-5, 1951, is a precursor to MIL-HDBK-5 and contains some useful data that was later removed. That data is still valid, and this is a good source.
5. Astronautics Structures Manual, NASA MSFC (Marshall Space Flight Center), 1975, is very good for general structures. Since our round and streamline tubes are easier than some more complicated shapes, we don’t need this unless things are getting complicated. Then it’s very helpful. But just remember to check your structure for crippling as well as column buckling.
6. Design of Wood Aircraft Structures, ANC-18, June 1951, covers wood in detail. But it goes beyond that to include structural analysis methods that are applicable to aircraft in general. Even if you’re not designing with wood, you should find a copy of this.
7. Another good general-purpose reference is Bell’s clear Structural Design Manual.