For the last few months we have been looking at gyroplanes. This month we turn our attention to pitch stability and control.
In flight, a gyroplane is suspended by the upward thrust of its autorotating rotor. As we discussed last month, the rotor blades can flap or teeter, and accordingly, the rotor cannot transmit a moment directly to the mast through the shaft.
The stick commands the angle of the rotor plane of rotation relative to the body of the gyroplane. By positioning the stick, the pilot determines the direction of rotor thrust vector (RTV).
For the purposes of this article, I am defining the “body” of the gyroplane as everything hanging from the rotor. The body of a typical gyroplane has no aerodynamic controls, and the pilot therefore is only controlling the body attitude indirectly, by aiming the rotor thrust. The attitude and pitch acceleration of the body will be determined by the orientation of the RTV relative to the center of gravity (CG) of the body, the aerodynamic forces acting on the body itself as a result of its shape and angle of attack, and the thrust vector of the engine and propeller.
This is a significant difference from early autogiros. Before the advent of direct control of the rotor, autogiros were controlled in pitch by airplane-style elevators on the horizontal tail. The orientation of the rotor axis of rotation, and hence the rotor’s plane of rotation relative to the rest of the gyro, was fixed. This arrangement worked well as long as there was a significant forward airspeed, but gave very little control at low airspeeds and in steep, slow descents.
The stability and control characteristics of a “modern” gyroplane configuration that is controlled by aiming the rotor thrust are quite different than those of a classical autogiro. This is particularly true for the Bensen-style machines with no horizontal tail.
The analysis that follows is a significantly simplified look at the quasi-static pitch trim and stability of a gyroplane. It neglects the effects of detailed rotor dynamics and blade flapping, but is sufficiently accurate to illustrate some important phenomena.
Initially, we will consider a gyroplane with no horizontal tail and the engine/propeller thrust line oriented directly through the center of gravity to remove thrust-induced effects. To further simplify the analysis, the body is assumed to generate no aerodynamic pitching moment and to have neutral aerodynamic pitch stability without the rotor.
Trim
In order for the vehicle to be in trim, the sum of all of the moments acting about the CG must be zero. In our simplified gyroplane, the weight acts downwards through the CG, and the rotor thrust acts on the mast in a direction normal to the rotor plane of rotation.
In order for the vehicle to be in trim, the rotor must be oriented so the RTV passes through the CG. The steady-state orientation of the rotor in level flight will be tilted backwards relative to the direction of flight to produce a positive angle of attack on the rotor disk. Because of this, the CG of the body will be somewhat forward of the mast so that the line from the rotor hub to the CG is normal to the rotor disc at cruise.
In steady-state trimmed flight, the RTV passes directly through the CG. If the rotor is tilted back further, so the RTV passes ahead of the CG, there will be a net nose-up moment causing the nose to accelerate upwards, and if the rotor is tilted back less, there will be a net nose-down moment, and the nose will pitch down.
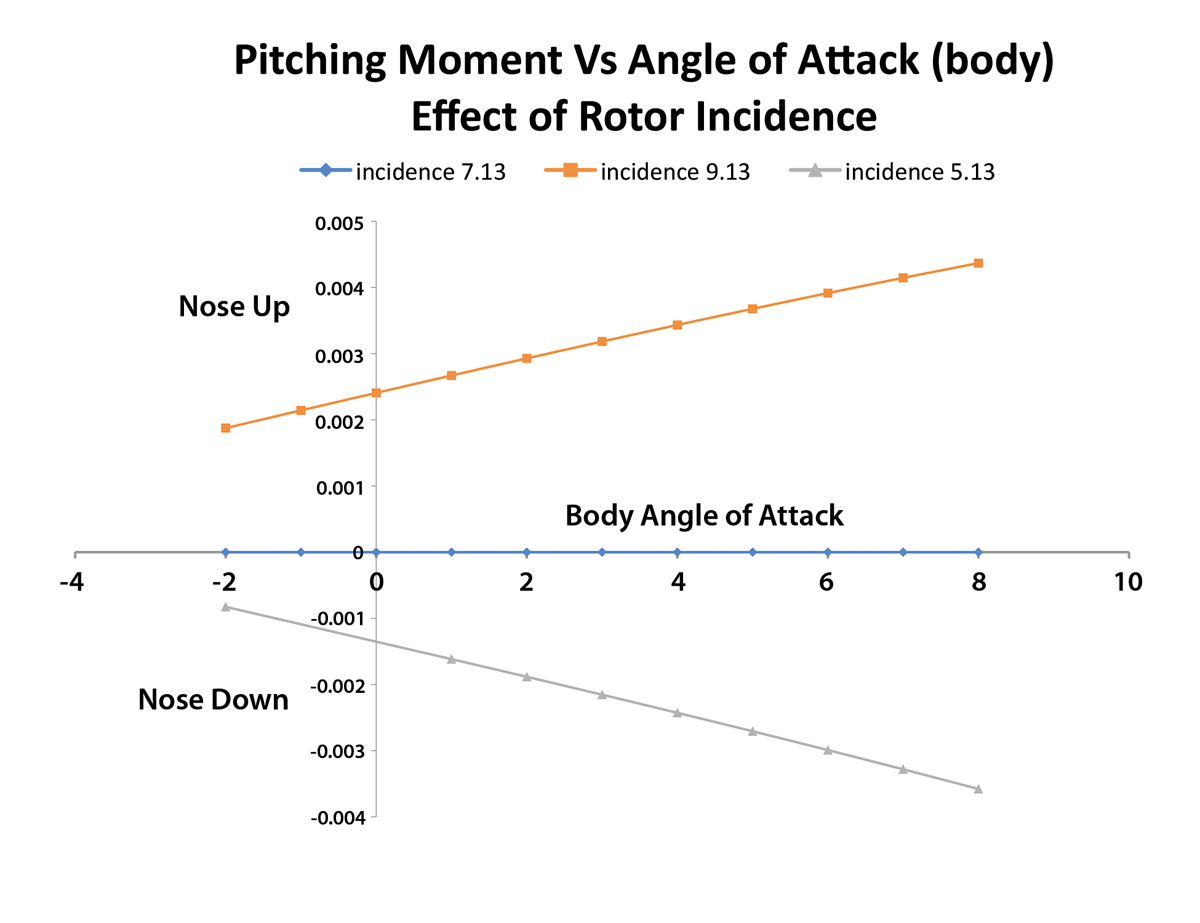
The effect of this is illustrated in Figure 1, which shows the pitching moment of our example gyroplane at three different rotor tilt angles (rotor incidence) as a function of body angle of attack.
Look first at the line for 7.13 degrees rotor incidence. This is the rotor orientation at which the vehicle is in trim. The CG has been placed far enough forward of the mast to put the machine in trim with the body at zero angle of attack in cruise. The 7.13-degree angle is the tilt-back angle that a relatively efficient rotor (rotor L/D=8) will have when flown at its best L/D.
The net pitching moment is zero at zero body angle of attack as intended. Importantly, it is also zero at all other angles of attack. This is because, unlike a wing, a rotor generates its net force normal to the plane of rotation so the RTV rotates with the vehicle as pitch attitude changes, and its direction relative to the CG therefore does not change with vehicle angle of attack.
This is a crucial difference between a gyroplane and a trike. The lift of a wing acts essentially normal to the airstream. As angle of attack changes, even though the drag changes, the net resultant force vector of the wing remains close to the same orientation normal to the airstream. As the trike pitches nose up, for example, the center of gravity moves forward relative to the lift vector, which produces a stabilizing moment driving the nose back down. On a gyroplane, the rotor thrust vector rotates with the vehicle, and no stabilizing moment is produced.
What this means is that an ideal tailless gyroplane flying in trim is neutrally stable in pitch. It has no aerodynamic tendency to return to its original angle of attack if perturbed by a gust or a control input. The 7.13-degree rotor incidence plot in Figure 1 illustrates this. Changing vehicle angle of attack does not produce any change in pitching moment.
We now turn our attention to the two other lines on Figure 1. These represent the situation with the rotor tilted +2 and -2 degrees respectively from the trimmed setting.
Figure 1: With 7.13 degrees rotor incidence, the gyro is in trim. When the incidence is 9.13, the nose is pointed up, and with an incidence of 5.13, the nose is down.
Looking first at the upper curve, we see the result of the pilot pulling the stick aft to tilt the rotor back and raise the nose. The RTV will now be rotated aft relative to the rotor head, so it passes in front of the CG. Notice that at all angles of attack, there is a net nose-up pitching moment. Also, the magnitude of the moment increases with increasing angle of attack. These two effects mean that the aircraft has a net nose-up moment and is also unstable in pitch. If the pilot holds the stick in this position, the gyroplane will pitch nose up at an ever-increasing rate. It will not find a new trimmed equilibrium at a higher angle of attack and slower airspeed with the stick fixed in this position.
Looking at the bottom curve we see the effect of pushing the stick forward and holding it. The RTV is now tilted more forward and passes behind the CG. There is a net nose-down pitching moment that increases in magnitude with increasing angle of attack. This is stable, but the gyro is out of trim nose-down as long as there is positive (upward) rotor thrust. In upright positive-G flight, the gyro will pitch down at an ever-increasing rate with the stick held in this position. In this linearized analysis, there is a stable trim point at zero rotor thrust, but this is not achievable in the real world since the rotor rpm will decay and the rotor will become unstable in flapping long before this zero-G condition is reached.
Implications
The implications of these characteristics on longitudinal flying qualities are profound. On a stable airplane the pilot is commanding angle of attack with the stick. If the airplane is flying in a trimmed steady-state condition and the pilot wants to fly slower, the stick is pulled aft to a new position and held there. The airplane will respond by pitching up, and settling down in a trimmed condition at a higher angle of attack. To fly faster, the stick is pushed forward, and again, the airplane responds by pitching down to its new trimmed angle of attack and stabilizing there. The trimmed position of the stick moves steadily back as trimmed airspeed decreases, and each stick position uniquely trims the airplane at a specific angle of attack.
None of this is true for the gyroplane.
The pilot of a fixed-wing airplane or a trike is commanding a trimmed angle of attack with the position of the stick or control bar.
The pilot of the gyroplane is commanding a pitch acceleration with the stick. The gyroplane is only in trim at the single stick position where the RTV is going directly through the CG. At this position, the net moment is zero and the pilot is not commanding any pitching motion. Since the gyro is neutrally stable, if there is any pitch rate when the stick is at the trimmed position, the pitch rate will continue. To stop it, the pilot must tilt the rotor to create an opposing pitch acceleration and then move the stick back to the trimmed position when the pitch rate goes to zero.
Changing airspeed in a gyro is a multi-step process. The pilot must first move the stick in the direction of the desired pitch attitude change. This will cause the gyro to develop an ever-increasing pitch rate. As the nose approaches the desired attitude, the stick must be moved in the opposite direction, past the trim position to generate an opposite pitch acceleration to stop the pitch rate. As the pitch rate comes to zero (ideally at the desired attitude) the pilot must move the stick to the trimmed position to capture the attitude.
In flight, the pilot will be moving the stick continuously in a series of small inputs, first one way and then the other, to keep the pitch rate near zero and hold attitude. Since the gyro is neutrally stable, pitch rates will not die off by themselves, and the pilot will be called on to actively augment pitch stability at all times.
There are several ways this can lead to trouble.
First, a fixed-wing pilot’s instincts do not apply to a gyroplane. A fixed-wing pilot who does not understand the difference will likely end up overcontrolling and chasing the pitch attitude when transitioning into the gyro.
Second, as airspeed increases, the mount of pitch acceleration commanded by a given stick motion will increase proportional to airspeed squared. This means that the pitch control will rapidly get more sensitive as airspeed increases. A machine that responds relatively slowly in slow flight will respond much more quickly in cruise. As the pitch sensitivity increases, the speed of the pilot’s response to any pitch rate must increase accordingly, and it will become increasingly difficult for the pilot to keep up.
If the pilot’s responses fall behind the actions of the gyro, the combination of the gyro’s characteristics and the pilot’s inputs will lead to a pitch oscillation that can quickly diverge to the point where, at the nose-down extreme of the oscillation, the rotor blades flap down far enough to hit the tail or the propeller, leading to catastrophe.
It’s easy to see how a pilot with little gyro experience, or a pilot exploring higher flight speed than he has flown before, can get into trouble quickly.
So far, we have only considered an idealized machine with no tail, and the thrust line passing through CG. Next month we will begin to explore how other configuration features affect flying qualities.