In the past few months, we have been looking at the various factors that affect the longitudinal balance of an airplane. We have seen how the arrangement of the fixed and variable masses of the airplane’s components and contents affect the position of the CG. Last month, we took a look at how the geometry of the horizontal tail affects the forward and aft limits of CG position for safe flight. Now it’s time to combine these factors to determine the tail size for the airplane we are designing.
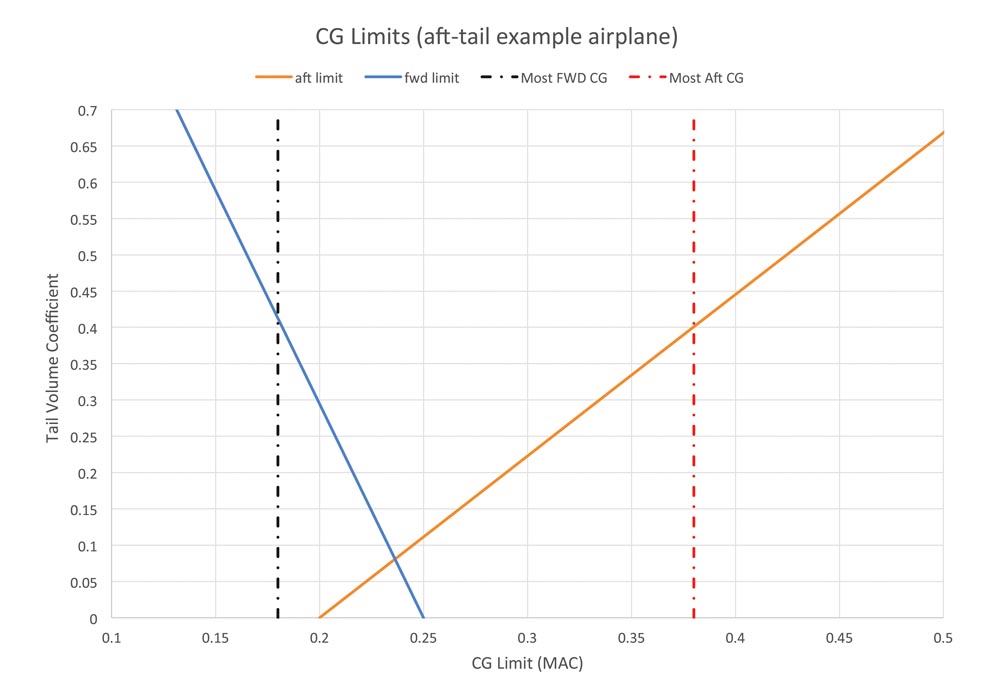
Last month, we were introduced to the “scissors” plot that shows the variation of forward and aft CG limits as a function of tail volume coefficient. Such a plot, for the same example airplane as used last month, is shown in Figure 1. There are now two additional vertical lines on the figure, which represent the most forward and most aft physical CG positions the airplane might be loaded to during operations. In this first example, the CG can be anywhere between a most forward position of 18% MAC (mean aerodynamic chord) and 38% MAC. The tail must be sized so that the airplane is safe to fly for any CG position inside this range.
Figure 1: In this example, the CG can be anywhere between a most forward position of 18% MAC (mean aerodynamic chord) and 38% MAC. The tail must be sized so that the airplane is safe to fly for any CG position inside this range.
CG Range and Tail Size
Tail size can be determined by looking at the intersections of the most extreme CG position lines and the lines representing the aerodynamic limits.
The “most forward CG” vertical line intersects the forward aerodynamic limit line at a tail volume coefficient of about 0.41.
The “most aft CG” vertical line intersects the aft aerodynamic limit line at a tail volume coefficient of 0.40.
Since the tail must be sized to accommodate flight at both the most forward and most aft CG positions, the correct tail volume coefficient is the larger of the two intersection points. In this case, the airplane must have a tail volume coefficient of at least 0.41.
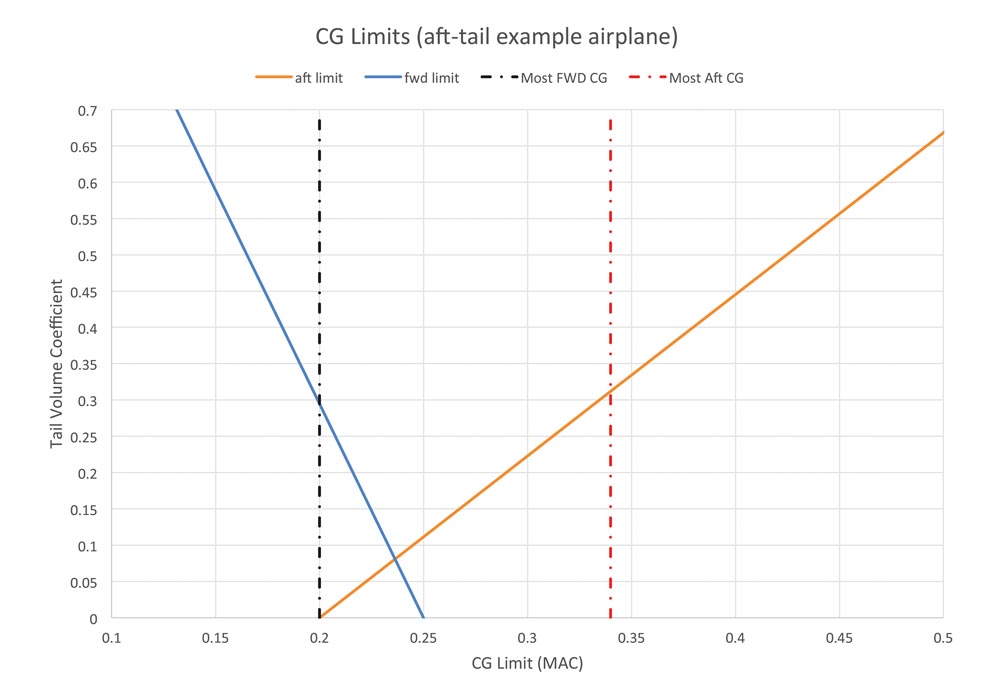
The absolute CG travel between the most forward and most aft CG positions affects how big the tail must be. Figure 2 represents the situation for the same example airplane with a reduced physical travel of the CG. For this example, the most forward CG is at 20% MAC, and the most aft CG is at 34% MAC.
Figure 2: The same airplane shown in Figure 1, but with a reduced physical travel of the CG. Now the most forward CG is at 20% MAC, and the most aft CG is at 34% MAC.
Now, the aft-limit intersection gives a tail volume coefficient of 0.32, and the forward-limit intersection gives a tail volume coefficient of 0.30. This version of the airplane needs the tail volume coefficient to be at least 0.32 to fly safely over its expected range of CG positions. Notice that this is almost 25% less than the 0.41 value required for the airplane in Figure 1. The reduction in CG travel means that the tail can be smaller and still provide adequate stability and control.
In general, the less the CG moves between its most forward and most aft physical positions, the less tail the airplane will need to fly safely. There are other aerodynamic considerations that will eventually end up sizing the tail to bigger than zero, even for an airplane with zero CG travel, but for most properly balanced conventional configurations, the physical travel of the CG is the strongest driver of tail size.
CG Range Position and Tail Size
Both of the airplanes in the previous examples were properly balanced designs. The position of the physical CG range was properly placed relative to the aerodynamic center of the configuration so that the tail sizes dictated by the most-forward CG and most-aft CG were close to the same. It is highly desirable to end up with a design that has this characteristic, but it’s not uncommon to find that the airplane is either nose-heavy or tail-heavy during an early design iteration.
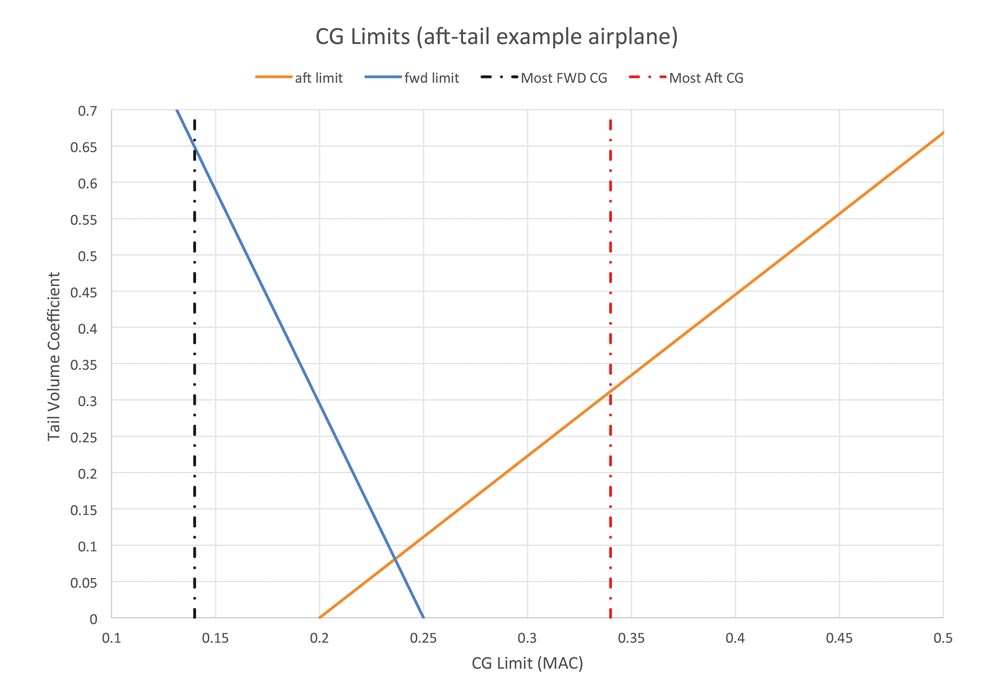
Figure 3: A nose-heavy airplane. It has the same 20% MAC difference between most-forward and most-aft CG positions, but the range has moved forward. Most-forward CG is now at 14% MAC, and most-aft CG is now at 34% MAC.
Nose-Heavy
Figure 3 shows the situation for a nose-heavy airplane. This airplane has the same 20% MAC difference between most-forward and most-aft CG positions, but the range has moved forward. Most-forward CG is now at 14% MAC, and most-aft at 34%. The effect on tail sizing is dramatic. Note that the tail sizes dictated by the two CG limits are now very different. The aft-CG limit dictated tail volume coefficient is 0.31, but the forward-CG limit dictated by tail volume coefficient has grown to 0.65. Since the minimum acceptable tail size is determined by the larger of the two, this airplane needs a tail volume coefficient of 0.65.
Notice that even though the total travel of the CG is the same as our first example, this new airplane requires a tail that is more than 35% larger. This is because the forward-CG requirements are stressing the tail more than in the more-balanced design, so even though the aft limit issues are less, the tail needs to be much larger to address the forward limit.
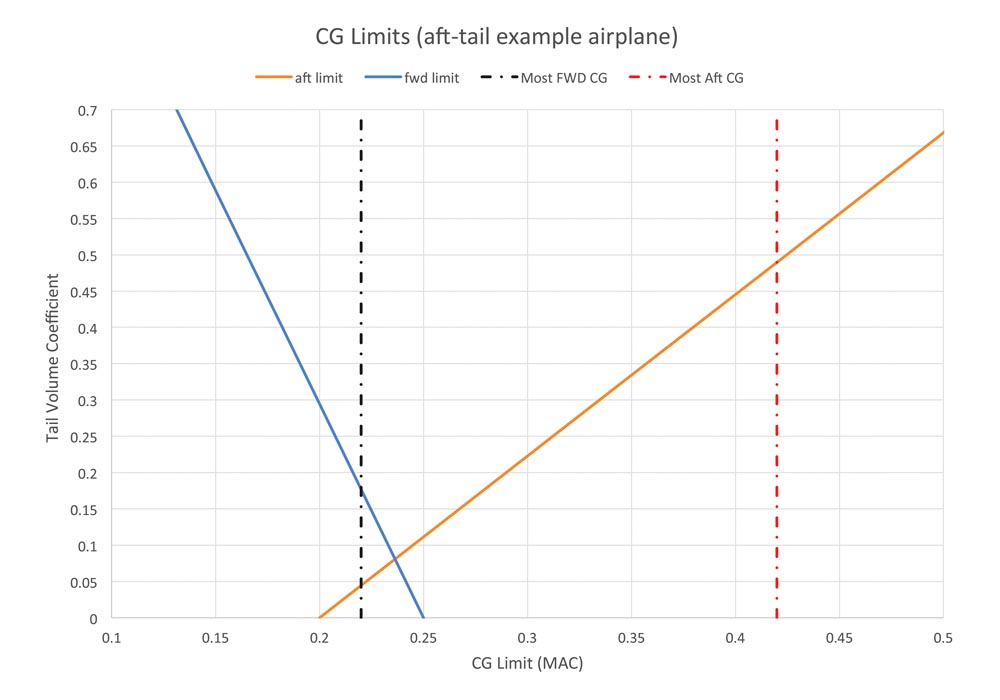
Figure 4: A tail-heavy airplane. Once again, the total CG travel is 20% MAC, but the most-forward CG is now at 22% MAC, and the most-aft at 42%.
Tail-Heavy
Figure 4 shows the situation for a tail-heavy airplane. Once again, the total CG travel is 20% MAC. The most-forward CG is now at 22% MAC, and the most-aft at 42%.
As with the nose-heavy case, the tail sizes dictated by the opposite ends of the CG envelope are different. This time, however, it is the aft limit that sets the tail size. The most-aft CG position requires a tail volume coefficient of 0.49, while the most-forward CG only requires 0.17.
Although this example is not as severe as our nose-heavy case above, it still requires a larger tail than the well-balanced case shown in Figure 1.
Making It Balance
A few observations for the designer:
First, keep the total CG travel as small as practically possible. This has multiple benefits. The tail will be smaller, cutting drag and weight. Also, the flying qualities of the airplane will vary less with how it is loaded.
If the airplane is nose-heavy or tail-heavy, it is worth some effort to cure this with the fundamentals of the configuration instead of simply band-aiding it with a bigger tail. Although all four airplanes in our examples would be safely flyable, the nose-heavy and tail-heavy airplanes are flawed designs.
If the airplane is out of balance this way, the designer has two general approaches available. The first is to rearrange the masses that make up the airplane and its contents to move the CG range to a better place relative to the aerodynamic limits of the configuration.
The second approach is to move the neutral point of the airplane to bring the aerodynamic limits to a position that is more in harmony with the existing mass properties. The most powerful way to do this is to move the position of the wing and its MAC to shift the aerodynamic center of the configuration.
If it is geometrically possible, the best way to accomplish this is to move the whole wing forward or aft. If structural or configuration integration issues force the position of the wing root to stay where it is, then some movement of the wing MAC can be achieved by changing the wing planform and introducing a modest amount of wing sweep.
One example of this approach is the swept-back upper wings seen on some biplanes. It’s desirable to have the root of the upper wing well forward of the cockpit so the wing does not interfere with entry and exit from the cockpit. This moves the wing far enough forward that the airplane will tend to be tail-heavy. By sweeping the upper wing back, the designer can move the aerodynamic center of the wings back to where it needs to be, while leaving the upper-wing root forward of the cockpit.
Although it is less common, there are some light airplanes that have a small amount of forward sweep to allow the wing carry-through structure to pass behind the pilot’s seat to allow the fuselage to be shallower. Examples of this design approach can be seen in the Cygnet experimental airplane and the Blkow Junior.